
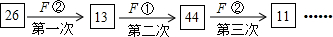
分析 根据运算规则进行重复计算,从中发现循环的规律,得到答案.
解答 解:根据题意,得
当n=2015时,第1次的计算结果是3n+5=6050;
第2次的计算结果是$\frac{6050}{2}$=3025;
第3次的计算结果是3025×3+5=9080;
第4次是计算结果是$\frac{9080}{{2}^{3}}$=1135;
第5次的计算结果是1135×3+5=3410;
第6次的计算结果是$\frac{3410}{2}$=1705,
第7次的计算结果是1705×3+5=5120,
第8次的计算结果是$\frac{5120}{{2}^{10}}$=5,
第9次的计算结果是5×3+5=20,
第10次的计算结果是$\frac{20}{{2}^{2}}$=5,开始循环.
故第2015次的计算结果是20.
故答案为:20.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律即可求出结果.


科目:初中数学 来源: 题型:解答题
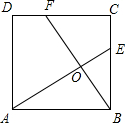 如图,两只蚂蚁分别位于一个正方形相邻的两个顶点A,B上,它们分别沿AE,BF的路线向BC和CD爬行,如果AE和BF相互垂直,那么它们爬行的距离相等吗?
如图,两只蚂蚁分别位于一个正方形相邻的两个顶点A,B上,它们分别沿AE,BF的路线向BC和CD爬行,如果AE和BF相互垂直,那么它们爬行的距离相等吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
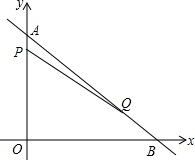 如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.
如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com