
 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).分析 (1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数;
(3)根据A,B,C的运动情况即可确定AB,BC的变化情况,即可确定AB-BC的值.
解答 解:(1)∵|a+2|+(b-1)2=0,
∴a=-2,b=1,
∴线段AB的长为:1-(-2)=3;
(2)存在.
由方程2x-2=$\frac{1}{2}$x+2,得x=$\frac{8}{3}$,
所以点C在数轴上对应的数为$\frac{8}{3}$.
设点P对应的数为m,
若点P在点A和点B之间,m-(-2)+1-m=$\frac{8}{3}$-m,解得m=-$\frac{1}{3}$;
若点P在点A左边,-2-m+1-m=$\frac{8}{3}$-m,解得m=-$\frac{11}{3}$.
所以P对应的数为-$\frac{1}{3}$或-$\frac{11}{3}$.
(3)A′B′-B′C′=(5t+3)-(5t+$\frac{5}{3}$)=$\frac{4}{3}$,
所以AB-BC的值随着时间t的变化而不变.
点评 此题考查一元一次方程的实际运用,以及数轴与绝对值,正确理解AB,BC的变化情况是关键.


科目:初中数学 来源: 题型:解答题
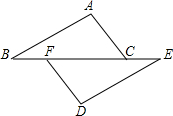 如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,AB=DE,
如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,AB=DE,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
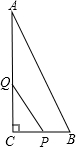 如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从点C出发沿着CB方向以1cm/s的速度运动,另一动点Q从A出发沿着AC边以2cm/s的速度运动,P,Q两点同时出发,运动时间为t(s).
如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从点C出发沿着CB方向以1cm/s的速度运动,另一动点Q从A出发沿着AC边以2cm/s的速度运动,P,Q两点同时出发,运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个篮球场的面积 | B. | 一张乒乓球台台面的面积 | ||
| C. | 《钱江晚报》一个版面的面积 | D. | 《数学》课本封面的面积 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -0.1是-0.001的立方根 | B. | 8的立方根为2 | ||
| C. | $\root{3}{216}$=-6 | D. | -27的立方根为-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+x)2=57 | B. | 1+x+x2=57 | C. | (1+x)x=57 | D. | 1+x+2x=57 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com