
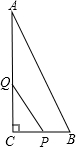
 如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从点C出发沿着CB方向以1cm/s的速度运动,另一动点Q从A出发沿着AC边以2cm/s的速度运动,P,Q两点同时出发,运动时间为t(s).
如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从点C出发沿着CB方向以1cm/s的速度运动,另一动点Q从A出发沿着AC边以2cm/s的速度运动,P,Q两点同时出发,运动时间为t(s).分析 (1)根据三角形的面积公式可以得出△ABC面积为$\frac{1}{2}$×4×8=16,△PCQ的面积为$\frac{1}{2}$t(8-2t),由题意列出方程解答即可;
(2)由等量关系S△PCQ=$\frac{1}{2}$S△ABC列方程求出t的值,但方程无解.
解答 解:(1)∵S△PCQ=$\frac{1}{2}$t(8-2t),S△ABC=$\frac{1}{2}$×4×8=16,
∴$\frac{1}{2}$t(8-2t)=16×$\frac{1}{4}$,
整理得t2-4t+4=0,
解得t=2.
答:当t=2s时△PCQ的面积为△ABC面积的$\frac{1}{4}$;
(2)当S△PCQ=$\frac{1}{2}$S△ABC时,
$\frac{1}{2}$t(8-2t)=16×$\frac{1}{2}$,
整理得t2-4t+8=0,
△=(-4)2-4×1×8=-16<0,
∴此方程没有实数根,
∴△PCQ的面积不可能是△ABC面积的一半.
点评 本题考查一元二次方程的应用,三角形的面积,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
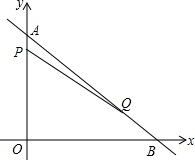 如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.
如图,在平面直角坐标系中,点A、点B分别在y轴、x轴的正半轴上,且满足$\sqrt{OA-30}$+(OB-40)2=0,若点P从A点出发,以每秒2个单位长度的速度沿线段AO运动,同时点Q从B点出发,以每秒5个单位长度的速度沿线段BA运动,连接PQ,点P,Q的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com