
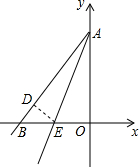
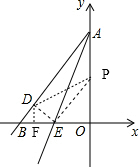
 已知如图,直线AE:y=3x+12交x轴于E点,交y轴于A点,再把△AOE沿着AE翻折,使得AO落在AD的位置,设直线AD交轴x于点B,P点以1个单位每秒的速度自B点出发沿BO-OA向终点A运动,设点P的运动时间为t.
已知如图,直线AE:y=3x+12交x轴于E点,交y轴于A点,再把△AOE沿着AE翻折,使得AO落在AD的位置,设直线AD交轴x于点B,P点以1个单位每秒的速度自B点出发沿BO-OA向终点A运动,设点P的运动时间为t. 时,求t的值,并判断此时以P点为圆心,以
时,求t的值,并判断此时以P点为圆心,以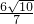 为半径的圆与直线AE的位置关系.
为半径的圆与直线AE的位置关系. =
=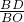 =
= =
=
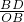 =
=
 =
=
 ,b=12
,b=12 x+12
x+12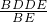 =
= =
=
 PE•DF=
PE•DF= (5-t)×
(5-t)× =-
=- t+6(0≤t<5)
t+6(0≤t<5)
 PE•DF=
PE•DF= (t-5)×
(t-5)× =
= t-6(5≤t<9)
t-6(5≤t<9)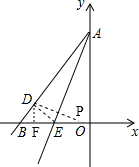
 x+12可知,当y=
x+12可知,当y= 时,x=-
时,x=- ,即点D的坐标为(-
,即点D的坐标为(- ,
, )
) ×OP•OE-
×OP•OE- ×AP•OF=48-
×AP•OF=48- (t-9)×4-
(t-9)×4- ×(21-t)×
×(21-t)× =
=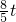 -
-
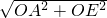 =4
=4
 =
=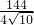 =
=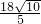 EN=AE-AN=4
EN=AE-AN=4 -
-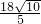 =
= ON=DN=
ON=DN= AN=
AN=
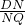 =
=
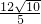

 PG
PG PG=
PG= PG
PG
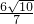 GE=
GE=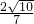
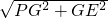 =
=
 即t=
即t=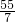
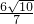
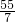 时,以P点为圆心,以
时,以P点为圆心,以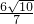 为半径的圆与直线AE相切.
为半径的圆与直线AE相切.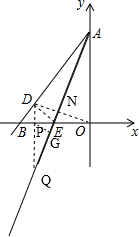



 即PM=
即PM=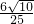

 PM=
PM=
 即t=
即t=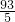
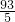 时,以P点为圆心,以
时,以P点为圆心,以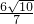 为半径的圆与直线AE相交.
为半径的圆与直线AE相交.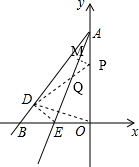
 x+12.
x+12. PE•DF,此时PE有两种表示情况:①PE=5-t,②PE=t-5,所以可求出S的两种情况,当点P在线段OA上时,△PDE的面积S=S四边形ADEO-S△POE-S△ADP=2S△AOE-
PE•DF,此时PE有两种表示情况:①PE=5-t,②PE=t-5,所以可求出S的两种情况,当点P在线段OA上时,△PDE的面积S=S四边形ADEO-S△POE-S△ADP=2S△AOE- ×OP•OE-
×OP•OE- ×AP•OF,此时OP=t-9,AP=OB+OA-t=21-t,代入即可求得S的第三种情况.
×AP•OF,此时OP=t-9,AP=OB+OA-t=21-t,代入即可求得S的第三种情况. ,可知tan∠DQN=
,可知tan∠DQN=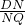 =
= ,满足这个条件的点P有两个,分别在直线AE的左右两侧.利用点D,O关于直线AE对称,连接OD,可得AE⊥OD,DN=ON,AE=4
,满足这个条件的点P有两个,分别在直线AE的左右两侧.利用点D,O关于直线AE对称,连接OD,可得AE⊥OD,DN=ON,AE=4 ,从而求出AN=
,从而求出AN=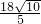 ,EN=AE-AN=
,EN=AE-AN= ,ON=
,ON= ,NQ=2DN=
,NQ=2DN=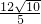 ,分两种情况讨论:①当点P在直线AE左侧时,过点P做PG⊥AE于G,则QG=2PG,根据tan∠GPE=tan∠OAE=
,分两种情况讨论:①当点P在直线AE左侧时,过点P做PG⊥AE于G,则QG=2PG,根据tan∠GPE=tan∠OAE= 求得t=
求得t=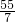 ,PG=
,PG=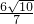 从而判断以P点为圆心,以
从而判断以P点为圆心,以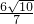 为半径的圆与直线AE位置关系为相切.②当点P在直线AE右侧时,过点P作PM⊥AE于点M根据tan∠MQP=tan∠DQN=
为半径的圆与直线AE位置关系为相切.②当点P在直线AE右侧时,过点P作PM⊥AE于点M根据tan∠MQP=tan∠DQN= ,tan∠PAM=
,tan∠PAM= 可求出PM=
可求出PM=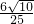 ,t=
,t=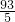 ,则可判断以P点为圆心,以
,则可判断以P点为圆心,以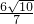 为半径的圆与直线AE位置关系为相交.
为半径的圆与直线AE位置关系为相交.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
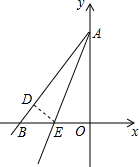 已知如图,直线AE:y=3x+12交x轴于E点,交y轴于A点,再把△AOE沿着AE翻折,使得AO落在AD的位置,设直线AD交轴x于点B,P点以1个单位每秒的速度自B点出发沿BO-OA向终点A运动,设点P的运动时间为t.
已知如图,直线AE:y=3x+12交x轴于E点,交y轴于A点,再把△AOE沿着AE翻折,使得AO落在AD的位置,设直线AD交轴x于点B,P点以1个单位每秒的速度自B点出发沿BO-OA向终点A运动,设点P的运动时间为t.| 1 |
| 2 |
6
| ||
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
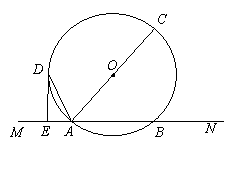
已知如图,直线MN交⊙O于A、B两点,AC是直径,AD平分![]() CAM交⊙O于D,过D作DE
CAM交⊙O于D,过D作DE![]() MN于E.
MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com