
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψBΘ®aΘ§bΘ©‘ΎΒΎ“ΜœσœόΘ§ΙΐBΉςBAΓΆy÷α”ΎAΘ§ΙΐBΉςBCΓΆx÷α”ΎCΘ§«“ Β ΐaΓΔb¬ζΉψΘ®a-b-2Θ©2+|2a+b-10|Γή0Θ§Κ§45Ϋ«ΒΡRtΓςDEFΒΡ“ΜΧθ÷±Ϋ«±ΏDF”κx÷α÷ΊΚœΘ§DEΓΆx÷α”ΎDΘ§ΒψF”κΉχ±ξ‘≠Βψ÷ΊΚœΘ§DE=DF=3Θ°ΓςDEF¥”Ρ≥ ±ΩΧΩΣ Φ―ΊΉ≈Ήχ±ξ÷α“‘1ΗωΒΞΈΜ≥ΛΕ»ΟΩΟκΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣtΟκΘ°
Θ®1Θ©«σΒψBΒΡΉχ±ξΘΜ
Θ®2Θ©»τΓςDEF―ΊΉ≈y÷αΗΚΖΫœρ‘ΥΕ·Θ§Ν§Ϋ”AEΘ§EGΤΫΖ÷ΓœAEFΘ§EHΤΫΖ÷ΓœAEDΘ§Β±EGΓΈDF ±Θ§«σΓœHEFΒΡΕ» ΐΘΜ
Θ®3Θ©»τΓςDEF―ΊΉ≈x÷α’ΐΖΫœρ‘ΥΕ·Θ§‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§Φ«ΓςAEF”κ≥ΛΖΫ–ΈOABC÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§Β±0ΘΦtΓή4Θ§S=![]() ±Θ§«κΡψ«σ≥ω‘ΥΕ· ±ΦδtΘ°
±Θ§«κΡψ«σ≥ω‘ΥΕ· ±ΦδtΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©BΘ®4Θ§2Θ©ΘΜΘ®2Θ©ΓœHEF==22.5ΓψΘΜΘ®3Θ©t=1Μρ4s.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”ΟΖ«ΗΚ ΐΒΡ–‘÷ Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®2Θ©Β±EGΓΈDF ±Θ§÷Μ“Σ÷ΛΟςΓœAWED=135ΓψΘ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΔΌ»γΆΦ2÷–Θ§Β±0ΘΦtΘΦ2 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςAPFΘ§S=![]() Θ®2-tΘ©t=t-
Θ®2-tΘ©t=t-![]() t2Θ§ΔΎ»γΆΦ3÷–Θ§Β±2ΘΦtΓή4 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPAFΘ§S=
t2Θ§ΔΎ»γΆΦ3÷–Θ§Β±2ΘΦtΓή4 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPAFΘ§S=![]() Θ®t-2Θ©2=t-2Θ§Ζ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®t-2Θ©2=t-2Θ§Ζ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΫβΘΚΘ®1Θ©ΓΏΘ®a-b-2Θ©2+|2a+b-10|Γή0Θ§
”÷ΓΏΘ®a-b-2Θ©2Γί0Θ§|2a+b-10|Γί0Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
ΓύBΘ®4Θ§2Θ©Θ°
Θ®2Θ©»γΆΦ1÷–Θ§…ηEGΫΜy÷α”ΎNΘ°
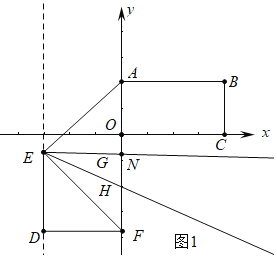
Β±EGΓΈDF ±Θ§ΓœNEF=ΓœEFD=45ΓψΘ§
ΓΏΓœAEF=90ΓψΘ§
ΓύΓœAEN=45ΓψΘ§
ÿDEøFNȧENøDFȧ
ΓύΥΡ±Ώ–ΈDENF «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓΏΓœEDF=90ΓψΘ§DE=DFΘ§
ΓύΥΡ±Ώ–ΈDENF «’ΐΖΫ–ΈΘ§
ΓύΓœDEN=90ΓψΘ§
ΓύΓœAED=135ΓψΘ§
ΓΏEHΤΫΖ÷ΓœAEDΘ§
ΓύΓœDEH=![]() ΓΝ135Γψ=67.5ΓψΘ§
ΓΝ135Γψ=67.5ΓψΘ§
ΓΏΓœDEF=45ΓψΘ§
ΓύΓœHEF=ΓœDEH-ΓœDEF=22.5ΓψΘ°
Θ®3Θ©ΔΌ»γΆΦ2÷–Θ§Β±0ΘΦtΘΦ2 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςAPFΘ§S=![]() Θ®2-tΘ©t=t-
Θ®2-tΘ©t=t-![]() t2Θ§
t2Θ§

”…Χβ“βΘΚt-![]() t2=
t2=![]() tȧ
tȧ
ΫβΒΟt=1Θ§Θ°
ΔΎ»γΆΦ3÷–Θ§Β±2ΘΦtΓή4 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPAFΘ§S=![]() Θ®t-2Θ©2=t-2Θ§
Θ®t-2Θ©2=t-2Θ§
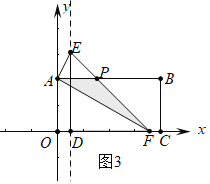
”…Χβ“βΘΚt-2=![]() tΘ§ΫβΒΟt=4Θ§
tΘ§ΫβΒΟt=4Θ§
Ήέ…œΥυ ωΘ§Β±t=1Μρ4s ±Θ§¬ζΉψΧθΦΰΘ§S=![]() tΘ°
tΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
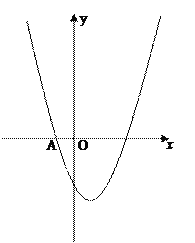
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏy=x2+bx©¹3Θ®b «≥Θ ΐΘ©Ψ≠ΙΐΒψAΘ®©¹1Θ§0Θ©Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΚΆΕΞΒψΉχ±ξΘΜ
Θ®2Θ©PΘ®mΘ§tΘ©ΈΣ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§PΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣP'Θ°
ΔΌ Β±ΒψP' ¬δ‘ΎΗΟ≈ΉΈοœΏ…œ ±Θ§«σmΒΡ÷ΒΘΜ
ΔΎ Β±ΒψP' ¬δ‘ΎΒΎΕΰœσœόΡΎΘ§P'A2»ΓΒΟΉν–Γ÷Β ±Θ§«σmΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «
A. ΓΑΟςΧλΫΒ”ξΒΡΗ≈¬ «80%Γ±±μ ΨΟςΧλ”–80%ΒΡ ±ΦδΕΦ‘ΎΫΒ”ξ
B. ΓΑ≈Ή“ΜΟΕ”≤±“’ΐΟφ≥·…œΒΡΗ≈¬ ΈΣ![]() Γ±±μ ΨΟΩ≈Ή2¥ΈΨΆ”–“Μ¥Έ’ΐΟφ≥·…œ
Γ±±μ ΨΟΩ≈Ή2¥ΈΨΆ”–“Μ¥Έ’ΐΟφ≥·…œ
C. ΓΑ≤ Τ±÷–Ϋ±ΒΡΗ≈¬ ΈΣ1%Γ±±μ Ψ¬ρ100’≈≤ Τ±ΩœΕ®Μα÷–Ϋ±
D. ΓΑ≈Ή“ΜΟΕ’ΐΖΫΧεςΜΉ”Θ§≥·…œΒΡΒψ ΐΈΣ2ΒΡΗ≈¬ ΈΣ![]() Γ±±μ ΨΥφΉ≈≈Ή÷ά¥Έ ΐΒΡ‘ωΦ”Θ§ΓΑ≈Ή≥ω≥·…œΒΡΒψ ΐΈΣ2Γ±’β“Μ ¬ΦΰΖΔ…ζΒΡΤΒ¬ Έ»Ε®‘Ύ
Γ±±μ ΨΥφΉ≈≈Ή÷ά¥Έ ΐΒΡ‘ωΦ”Θ§ΓΑ≈Ή≥ω≥·…œΒΡΒψ ΐΈΣ2Γ±’β“Μ ¬ΦΰΖΔ…ζΒΡΤΒ¬ Έ»Ε®‘Ύ![]() ΗΫΫϋ
ΗΫΫϋ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
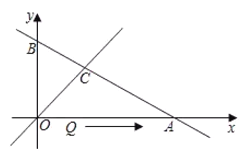
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏ![]() ”κΉχ±ξ÷αΖ÷±πΫΜ”ΎΒψ
”κΉχ±ξ÷αΖ÷±πΫΜ”ΎΒψ![]() Θ§”κ÷±œΏ
Θ§”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() «œΏΕΈ
«œΏΕΈ![]() …œΒΡΕ·ΒψΘ§Ν§Ϋ”
…œΒΡΕ·ΒψΘ§Ν§Ϋ”![]() Θ§»τ
Θ§»τ![]() «Β»―ϋ»ΐΫ«–ΈΘ§‘ρ
«Β»―ϋ»ΐΫ«–ΈΘ§‘ρ![]() ΒΡ≥ΛΈΣ___________Θ°
ΒΡ≥ΛΈΣ___________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Τϊ≥ΒΉ®¬τΒξœζ έAΘ§BΝΫ÷÷–ΆΚ≈ΒΡ–¬Ρή‘¥Τϊ≥Β.…œ÷ή έ≥ω1ΝΨA–Ά≥ΒΚΆ3ΝΨB–Ά≥ΒΘ§œζ έΕνΈΣ96Άρ‘ΣΘΜ±Ψ÷ή“― έ≥ω2ΝΨA–Ά≥ΒΚΆ1ΝΨB–Ά≥ΒΘ§œζ έΕνΈΣ62Άρ‘Σ.
Θ®1Θ©«σΟΩΝΨA–Ά≥ΒΚΆB–Ά≥ΒΒΡ έΦέΗςΈΣΕύ…ΌΆρ‘ΣΘΩ
Θ®2Θ©ΦΉΙΪΥΨΡβœρΗΟΒξΙΚ¬ρAΘ§BΝΫ÷÷–ΆΚ≈ΒΡ–¬Ρή‘¥Τϊ≥ΒΙ≤6ΝΨΘ§«“A–ΆΚ≈≥Β≤Μ…Ό”Ύ2ΝΨΘ§ΙΚ≥ΒΖ―≤Μ…Ό”Ύ130Άρ‘ΣΘ§‘ρ”–ΡΡΦΗ÷÷ΙΚ≥ΒΖΫΑΗΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΝΫΗω»ΪΒ»ΒΡΓςABCΚΆΓςDEF÷–Θ§ΓœACB=ΓœDFE=90ΓψΘ§AB=DEΘ§Τδ÷–ΒψBΚΆΒψD÷ΊΚœΘ§ΒψF‘ΎBC…œΘ§ΫΪΓςDEF―Ί…δœΏBCΤΫ“ΤΘ§…ηΤΫ“ΤΒΡΨύάκΈΣxΘ§ΤΫ“ΤΚσΒΡΆΦ–Έ”κΓςABC÷ΊΚœ≤ΩΖ÷ΒΡΟφΜΐΈΣyΘ§yΙΊ”ΎxΒΡΚ· ΐΆΦœσ»γΆΦ2Υυ ΨΘ®Τδ÷–0ΓήxΓήmΘ§mΘΦxΓή3Θ§3ΘΦxΓή4 ±Θ§Κ· ΐΒΡΫβΈω Ϋ≤ΜΆ§Θ©
Θ®1Θ©ΧνΩ’ΘΚBCΒΡ≥ΛΈΣ_____ΘΜ
Θ®2Θ©«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΟϊΕ”‘±≤ΈΦ”…δΜς―ΒΝΖΘ§≥…Φ®Ζ÷±π±Μ÷Τ≥…œ¬Ν–ΝΫΗωΆ≥ΦΤΆΦΘΚ

ΗυΨί“‘…œ–≈œΔΘ§’ϊάμΖ÷Έω ΐΨί»γœ¬ΘΚ
ΤΫΨυ≥…Φ®/ΜΖ | ÷–ΈΜ ΐ/ΜΖ | ÷Ύ ΐ/ΜΖ | ΖΫ≤ν | |
ΦΉ | a | 7 | 7 | 1.2 |
““ | 7 | b | 8 | c |
Θ®1Θ©–¥≥ω±μΗώ÷–aΘ§bΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©Ζ÷±π‘Υ”Ο±μ÷–ΒΡΥΡΗωΆ≥ΦΤΝΩΘ§Φρ“ΣΖ÷Έω’βΝΫΟϊΕ”‘±ΒΡ…δΜς―ΒΝΖ≥…Φ®Θ°»τ―Γ≈…Τδ÷–“ΜΟϊ≤Έ»ϋΘ§Ρψ»œΈΣ”Π―ΓΡΡΟϊΕ”‘±Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAB «Γ―OΒΡ÷±ΨΕΘ§BP «Γ―OΒΡœ“Θ§œ“CDΓΆAB”ΎΒψFΘ§ΫΜBP”ΎΒψGΘ§E‘ΎCDΒΡ―”≥ΛœΏ…œΘ§EP=EGΘ§

Θ®1Θ©«σ÷ΛΘΚ÷±œΏEPΈΣΓ―OΒΡ«–œΏΘΜ
Θ®2Θ©ΒψP‘ΎΝ”ΜΓAC…œ‘ΥΕ·Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§»τBG2=BFBOΘ° ‘÷ΛΟςBG=PGΘΜ
Θ®3Θ©‘Ύ¬ζΉψΘ®2Θ©ΒΡΧθΦΰœ¬Θ§“―÷ΣΓ―OΒΡΑκΨΕΈΣ3Θ§sinB=![]() Θ°«σœ“CDΒΡ≥ΛΘ°
Θ°«σœ“CDΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ≥θΕΰ ΐ―ß–Υ»Λ–ΓΉιΜνΕ· ±Θ§≈ωΒΫ’β―υ“ΜΒάΧβΘΚ
ΓΑ“―÷Σ’ΐΖΫ–Έ![]() Θ§Βψ
Θ§Βψ![]() Ζ÷±π‘Ύ±Ώ
Ζ÷±π‘Ύ±Ώ![]() …œΘ§»τ
…œΘ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() Γ±Θ°
Γ±Θ°
Ψ≠ΙΐΥΦΩΦΘ§¥σΦ“Ηχ≥ωΝΥ“‘œ¬ΝΫΗωΖΫΑΗΘΚ
Θ®ΦΉΘ©ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() ΘΜ
ΘΜ
Θ®““Θ©ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ής
Θ§Ής![]() ΫΜ
ΫΜ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() ΘΜΆ§―ßΟ«Υ≥άϊΒΊΫβΨωΝΥΗΟΧβΚσΘ§¥σΦ“ΉΝΡΞΉ≈œκΗΡ±δΈ ΧβΒΡΧθΦΰΘ§ΉςΗϋΕύΒΡΧΫΥςΘ°
ΘΜΆ§―ßΟ«Υ≥άϊΒΊΫβΨωΝΥΗΟΧβΚσΘ§¥σΦ“ΉΝΡΞΉ≈œκΗΡ±δΈ ΧβΒΡΧθΦΰΘ§ΉςΗϋΕύΒΡΧΫΥςΘ°
Θ®1Θ©Ε‘–ΓΫή”ωΒΫΒΡΈ ΧβΘ§«κ‘ΎΦΉΓΔ““ΝΫΗωΖΫΑΗ÷–»Έ―Γ“ΜΗωΘ§Φ”“‘÷ΛΟςΘ®»γΆΦ1Θ©ΘΜ


ΆΦ1 ΆΦ2
Θ®2Θ©»γΙϊΑ―ΧθΦΰ÷–ΒΡΓΑ![]() Γ±ΗΡΈΣΓΑ
Γ±ΗΡΈΣΓΑ![]() ”κ
”κ![]() ΒΡΦ–Ϋ«ΈΣ
ΒΡΦ–Ϋ«ΈΣ![]() Γ±Θ§≤ΔΦΌ…η’ΐΖΫ–Έ
Γ±Θ§≤ΔΦΌ…η’ΐΖΫ–Έ![]() ΒΡ±Ώ≥ΛΈΣlΘ§
ΒΡ±Ώ≥ΛΈΣlΘ§![]() ΒΡ≥ΛΈΣ
ΒΡ≥ΛΈΣ![]() Θ®»γΆΦ2Θ©Θ§ ‘«σ
Θ®»γΆΦ2Θ©Θ§ ‘«σ![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com