
【题目】某校初二数学兴趣小组活动时,碰到这样一道题:
“已知正方形![]() ,点
,点![]() 分别在边
分别在边![]() 上,若
上,若![]() ,则
,则![]() ”.
”.
经过思考,大家给出了以下两个方案:
(甲)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;
;
(乙)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;同学们顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.
;同学们顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.
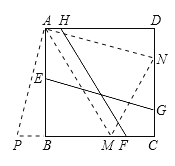
(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1);


图1 图2
(2)如果把条件中的“![]() ”改为“
”改为“![]() 与
与![]() 的夹角为
的夹角为![]() ”,并假设正方形
”,并假设正方形![]() 的边长为l,
的边长为l,![]() 的长为
的长为![]() (如图2),试求
(如图2),试求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)选乙,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,通过证△AMB≌△ADN来得出结论;
,通过证△AMB≌△ADN来得出结论;
(2)按(1)的思路也要通过构建全等三角形来求解,可过点A作AM∥HF交BC于点M,过点A作AN∥EG交CD于点N,将△AND绕点A旋转到△APB,不难得出△APM和△ANM全等,那么可得出PM=MN,而MB的长可在直角三角形ABM中根据AB和AM(即HF的长)求出.如果设DN=x,那么NM=PM=BM+x,MC=BCBM=1BM,因此可在直角三角形MNC中用勾股定理求出DN的长,进而可在直角三角形AND中求出AN即EG的长.
(1)证明:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]()
∴![]() ,
,![]() ,
,
∵正方形![]()
∴![]() ,
,![]() ,
,
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]() 即
即![]() .
.

(2)解:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
将![]() 绕点
绕点![]() 旋转到
旋转到![]() ,
,
∵![]() 与
与![]() 的夹角为
的夹角为![]()
∴![]()
∴![]() ,即
,即![]()
从而![]()
∴![]()
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
解得:![]()
∴![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,点B(a,b)在第一象限,过B作BA⊥y轴于A,过B作BC⊥x轴于C,且实数a、b满足(a-b-2)2+|2a+b-10|≤0,含45角的Rt△DEF的一条直角边DF与x轴重合,DE⊥x轴于D,点F与坐标原点重合,DE=DF=3.△DEF从某时刻开始沿着坐标轴以1个单位长度每秒的速度匀速运动,运动时间为t秒.
(1)求点B的坐标;
(2)若△DEF沿着y轴负方向运动,连接AE,EG平分∠AEF,EH平分∠AED,当EG∥DF时,求∠HEF的度数;
(3)若△DEF沿着x轴正方向运动,在运动过程中,记△AEF与长方形OABC重叠部分的面积为S,当0<t≤4,S=![]() 时,请你求出运动时间t.
时,请你求出运动时间t.

查看答案和解析>>
科目:初中数学 来源: 题型:
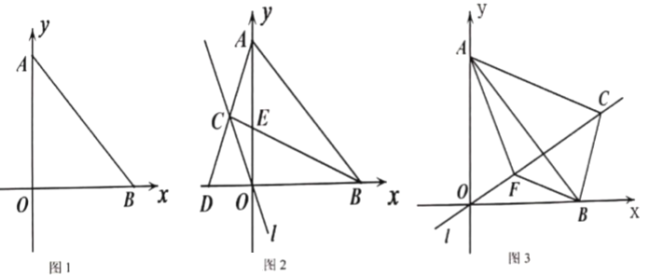
【题目】如图,平面直角坐标系中,![]() 、
、![]() ,且
,且![]() 、
、![]() 满足
满足![]()
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过点![]() 的直线
的直线![]() 上有一点
上有一点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,如图2,当点
,如图2,当点![]() 在第二象限时,
在第二象限时,![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,如图3,当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
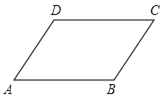
【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD.
(1)用直尺和圆规作出么ABC的平分线BE,交AD的延长线于点E,交DC于点F(保留作图痕迹,不写作法);
(2)求证:△ABE是等腰三角形;
(3)在(1)中所得图形中,除△ABE外,请你写出其他的等腰三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政公司为绿化建设路风景带,计划购买甲乙两种树苗600株,甲种树苗每株50元,乙种树苗每株70元.有关统计表明,甲乙两种树苗的成活率分别为80%和95%.(注:成活率=![]() ×100%).
×100%).
(1)若购买树苗的钱不超过40000元,应如何选购甲、乙两种树苗;
(2)若希望这批树苗的成活率不低于90%,且购买树苗的费用最低,应如何选购甲、乙两种树苗并求出最低费用是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).

(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过点(-1,0)且平行于y轴的直线.
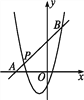
(1)求m,n的值;
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA∶PB=1∶5,求一次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com