
【题目】已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过点(-1,0)且平行于y轴的直线.
(1)求m,n的值;
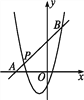
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA∶PB=1∶5,求一次函数的表达式.
【答案】(1)m=2,n=-2;(2)一次函数的表达式为y=x+4.
【解析】试题分析:(1)利用对称轴公式求得![]() ,把
,把![]() 代入二次函数
代入二次函数![]() 进而就可求得
进而就可求得![]() ;
;
(2)根据(1)得出二次函数的解析式,根据已知条件,利用平行线分线段成比例定理求得![]() 的纵坐标,代入二次函数的解析式中求得
的纵坐标,代入二次函数的解析式中求得![]() 的坐标,然后利用待定系数法就可求得一次函数的表达式.
的坐标,然后利用待定系数法就可求得一次函数的表达式.
试题解析:(1)由题意得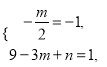 解得
解得![]()
(2)如图,分别过点P,B作x轴的垂线,垂足分别为C,D,则PC∥BD,
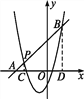
![]() △APC∽△ABD,
△APC∽△ABD,
![]()
![]() .
.
![]() PA∶PB=1∶5,PC=1,
PA∶PB=1∶5,PC=1,
![]()
![]() ,
,
![]() BD=6.
BD=6.
令x2+2x-2=6,
解得:x1=2,x2=-4(舍去),
![]() 点B坐标为(2,6),
点B坐标为(2,6),
![]()
![]() 解得
解得![]()
![]() 一次函数的表达式为y=x+4.
一次函数的表达式为y=x+4.


科目:初中数学 来源: 题型:
【题目】某校初二数学兴趣小组活动时,碰到这样一道题:
“已知正方形![]() ,点
,点![]() 分别在边
分别在边![]() 上,若
上,若![]() ,则
,则![]() ”.
”.
经过思考,大家给出了以下两个方案:
(甲)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;
;
(乙)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;同学们顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.
;同学们顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.
(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1);


图1 图2
(2)如果把条件中的“![]() ”改为“
”改为“![]() 与
与![]() 的夹角为
的夹角为![]() ”,并假设正方形
”,并假设正方形![]() 的边长为l,
的边长为l,![]() 的长为
的长为![]() (如图2),试求
(如图2),试求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )

A. 2![]() π B.
π B. ![]() π C. 2π D. 2
π C. 2π D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某校田径队25人年龄的平均数和中位数都是16岁,但是后来发现其中有一位同学的年龄登记错误,将17岁写成了19岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A. a>16,b=16 B. a>16,b<16 C. a<16,b<16 D. a<16,b=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形的对角线分别为 x、y,一边长为 12,则 x、y 的值可能是( )
A.8 与 14B.10 与 14C.18 与 20D.4 与 28
查看答案和解析>>
科目:初中数学 来源: 题型:
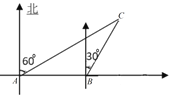
【题目】如图,某货船以24海里/时的速度将一批重要物资从![]() 处运往正东方向的M处,在点
处运往正东方向的M处,在点![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上.该货船航行
的方向上.该货船航行![]() 分钟后到达
分钟后到达![]() 处,此时再测得该岛在北偏东
处,此时再测得该岛在北偏东![]() 的方向上,已知在
的方向上,已知在![]() 岛周围
岛周围![]() 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,D、E、F是△ABC三边的中点,下列结论:①四边形AEDF,BDEF,CDFE都是平行四边形;②△ABC∽△DEF;③S△ABC=2S△DEF;④△DEF的周长是△ABC周长的一半,其中正确的序号是( )

A. ①②④ B. ①②③ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t(分钟)的变化规律有如下关系式:  (y值越大表示接受能力越强)
(y值越大表示接受能力越强)
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中;
(2)讲课开始后多少分钟,学生的注意力最集中能持续多少分钟;
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边的中点,点E,F分别在AC,AB上,且DE∥AB,EF∥BC.
(1)求证:CD=EF;
(2)已知∠ABC=60°,连接BE,若BE平分∠ABC,CD=6,求四边形BDEF的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com