
【题目】如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,

(1)求证:直线EP为⊙O的切线;
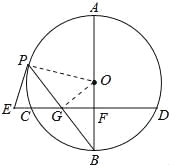
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BFBO.试证明BG=PG;
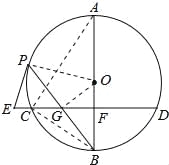
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=![]() .求弦CD的长.
.求弦CD的长.
【答案】(1)见解析;(2)见解析;(3)4![]() .
.
【解析】试题分析:(1)证明:连结OP,∵EP=EG,∴∠EPG=∠EGP,又∵∠EGP=∠BGF,∴∠EPG=∠BGF,∵OP=OB,∴∠OPB=∠OBP,∵CD⊥AB,∴∠BFG=∠BGF+∠OBP=90°,∴∠EPG+∠OPB=90°,∴直线EP为⊙O的切线;
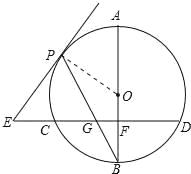
(2)证明:如图,连结OG,OP,∵BG2=BFBO,∴![]() =
=![]() ,∴△BFG∽△BGO,∴∠BGO=∠BFG=90°,由垂径定理知:BG=PG;
,∴△BFG∽△BGO,∴∠BGO=∠BFG=90°,由垂径定理知:BG=PG;
(3)解:如图,连结AC、BC、OG、OP,∵sinB=![]() ,∴
,∴![]() =
=![]() ,∵OB=r=3,∴OG=
,∵OB=r=3,∴OG=![]() ,由(2)得∠EPG+∠OPB=90°,∠B+∠BGF=∠OGF+∠BGF=90°,∴∠B=∠OGF,∴sin∠OGF=
,由(2)得∠EPG+∠OPB=90°,∠B+∠BGF=∠OGF+∠BGF=90°,∴∠B=∠OGF,∴sin∠OGF=![]() =
=![]() ,∴OF=1,∴BF=BO﹣OF=3﹣1=2,FA=OF+OA=1+3=4,在Rt△BCA中, CF2=BFFA,∴CF=
,∴OF=1,∴BF=BO﹣OF=3﹣1=2,FA=OF+OA=1+3=4,在Rt△BCA中, CF2=BFFA,∴CF=![]() =
=![]() =2
=2![]() .∴CD=2CF=4
.∴CD=2CF=4![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点B(a,b)在第一象限,过B作BA⊥y轴于A,过B作BC⊥x轴于C,且实数a、b满足(a-b-2)2+|2a+b-10|≤0,含45角的Rt△DEF的一条直角边DF与x轴重合,DE⊥x轴于D,点F与坐标原点重合,DE=DF=3.△DEF从某时刻开始沿着坐标轴以1个单位长度每秒的速度匀速运动,运动时间为t秒.
(1)求点B的坐标;
(2)若△DEF沿着y轴负方向运动,连接AE,EG平分∠AEF,EH平分∠AED,当EG∥DF时,求∠HEF的度数;
(3)若△DEF沿着x轴正方向运动,在运动过程中,记△AEF与长方形OABC重叠部分的面积为S,当0<t≤4,S=![]() 时,请你求出运动时间t.
时,请你求出运动时间t.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对.正确处置,顺利返航,避免了一场灾难的发生,下面表格是成都当日海拔高度h(千米)与相应高度处汽温t(℃)的关系(成都地处四川盆地,海拔高度较低,为方便计算,在此题中近似为0米).
海拔高度h(千米) | 0 | 1 | 2 | 3 | 4 | 5 | … |
气温t(℃) | 20 | 14 | 8 | 2 | -4 | -1 | … |
根据上表,回答以下问题:
(1)由上表可知海拔5千米的上空气温约为______℃;
(2)由表格中的规律请写出当日气温t与海拔高度h的关系式为______.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用的时间关系图.根据图象回答以下问题:
(3)挡风玻璃在高空爆裂时飞机所处的高度为______千米,返回地面用了______分钟;
(4)飞机在2千米高空水平面上大约盘旋了______分钟;
(5)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为______℃,由此可见机长在高空经历了多大的艰险.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

查看答案和解析>>
科目:初中数学 来源: 题型:
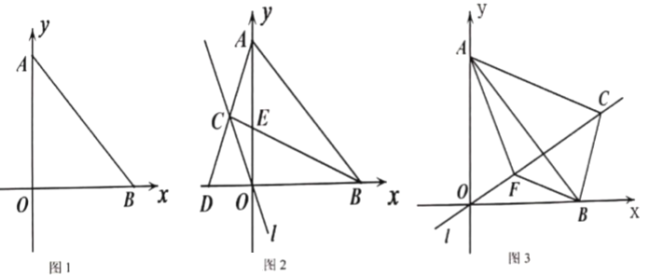
【题目】如图,平面直角坐标系中,![]() 、
、![]() ,且
,且![]() 、
、![]() 满足
满足![]()
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过点![]() 的直线
的直线![]() 上有一点
上有一点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,如图2,当点
,如图2,当点![]() 在第二象限时,
在第二象限时,![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,如图3,当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).

(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com