
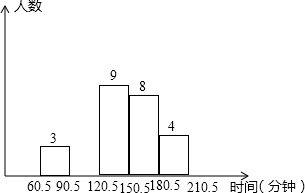
 某校为了了解本校九年级学生一天中在家里做作业所用的时间,随机抽查了该校九年级的40名,并把调查所得的所有数据(时间)进行整理,分成五组,绘制成统计图(如图).
某校为了了解本校九年级学生一天中在家里做作业所用的时间,随机抽查了该校九年级的40名,并把调查所得的所有数据(时间)进行整理,分成五组,绘制成统计图(如图).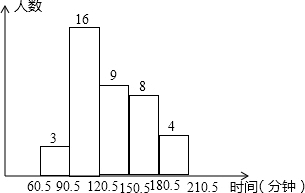 解:(1)①这个样本的样本容量为40;
解:(1)①这个样本的样本容量为40;| 3 |
| 40 |
| 16 |
| 40 |
| 9 |
| 40 |
| 8 |
| 40 |
| 4 |
| 40 |


科目:初中数学 来源: 题型:
| A、70.31×108 |
| B、7.031×109 |
| C、7031106 |
| D、7.031×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 你喜欢玩游戏吗?现在请你玩一个转盘游戏,如图所示的两个转盘中,指针落在每个数字上机会均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针指向一个数字,用所指的两个数字作乘积,请你求出数字之积为奇数的概率.( )
你喜欢玩游戏吗?现在请你玩一个转盘游戏,如图所示的两个转盘中,指针落在每个数字上机会均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针指向一个数字,用所指的两个数字作乘积,请你求出数字之积为奇数的概率.( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com