
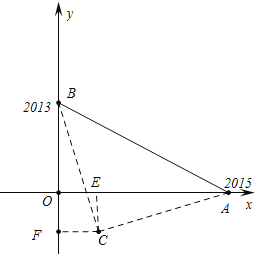
【题目】已知,在平面直角坐标系中,点A(2015,0)、B(0,2013),以AB为斜边在直线AB下方作等腰直角△ABC,则点C的坐标为 .
【答案】(1,﹣1).
【解析】
试题分析:如图设△CAB是等腰直角三角形,点C坐标(x,y),作CE⊥OA于E,CF⊥OB于F,先证明△ACE≌△BCF,推出四边形OECF是正方形,列出方程即可解决问题.
解:如图设△CAB是等腰直角三角形,点C坐标(x,y),作CE⊥OA于E,CF⊥OB于F.
∵∠CEO=∠CFO=∠EOF=90°.
∴四边形OECF是矩形,
∴CE=OF,PF=OE,∠ECF=90°,
∵∠ECF=∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,
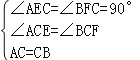 ,
,
∴△ACE≌△BCF,
∴CE=CF,AE=BF,
∴四边形OECF是正方形,
∴x=﹣y,2013+x=2015﹣x,
∴x=1,y=﹣1,
∴点C坐标(1,﹣1).
故答案为(1,﹣1).


科目:初中数学 来源: 题型:
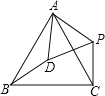
【题目】如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过一次逆时针旋转后到△ACP的位置,则旋转中心是 ,旋转角等于 °,△ADP是 三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,射线OA绕点O以每秒钟6°的速度逆时针旋转到OP,设射线OA旋转OP所用时间为t秒(t<30).
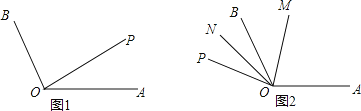
(1)如图1,直接写出∠BOP= °(用含t的式子表示);
(2)若OM平分∠AOP,ON平分∠BOP.
①当OA旋转到如图1所示OP处,请完成作图并求∠MON的度数;
②当OA旋转到如图2所示OP处,若2∠BOM=3∠BON,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧![]() (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )

A.r B.![]() r C.2r D.
r C.2r D.![]() r
r
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com