解:(1)3x-2=5x+4,
移项,合并同类项,得
-2x=6,
系数化为1,得
x=-3.
(2)

[

(x-1)-3]=2x-5,
先去中括号,得
(x-1)-2=2x-5,
去小括号,得
x-1-2=2x-5,
移项,合并同类项,得
-x=-2,
系数化为1,得
x=2.
(3)

,
去分母,得
3(3x-1)=12-4(x+3),
去括号,得
9x-3=12-4x-12,
移项,合并同类项,得
13x=-3,
系数化为1,得
x=-
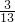
.
(4)

,
将方程变形为

+2x=2,
去分母,得
5(0.5x-0.1)+2x=2,
去括号,得
2.5x-0.5+2x=2,
移项,合并同类项,得
4.5x=2.5,
系数化为1,得
x=

.
(5)

,
将2x-3y=5两边同乘以3,得
6x-9y=15 ①,
用6x+5y=1减去①,得
14y=-14,
y=-1,
将y=-1代入2x-3y=5,得
2x+3=5,
2x=2,
x=1.
所以这个方程组的解是
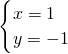
;
(6)

,
将4x-

y=-1两边同乘以9,得
36x-3y=-9 ①,
用①减去x-3y=-9,得
35x=0,
x=0,
将x=0代入x-3y=-9,得
y=3.
所以这个方程组的解是

.
分析:(1)将方程移项,合并同类项,系数化为1,即可求解;
(2)先去中括号,再去小括号,计算比较简便;
(3)将方程去分母,去括号,然后将方程移项,合并同类项,系数化为1,即可求解;
(4)先将分母化为整数,然后计算比较简便;
(5)将2x-3y=5两边同乘以3,然后与另一个方程相减消去x,解得y,再将y的值代入,即可解得x;
(6)将4x-

y=-1两边同乘以9,然后与另一个方程相减消去y,解得x,再将x的值代入,即可解得y.
点评:解一元一次方程的基本思路是:通过对方程变形,把含有未知数的项移到方程的一边,把常数项移到方程的另一边,最终把方程“转化”为x=a(a为常数)的形式.
解二元一次方程组的基本思路是通过加减法或代入法去掉其中的一个未知数,求出另一个未知数的解,进而求出另一个未知数的解.

 [
[ (x-1)-3]=2x-5
(x-1)-3]=2x-5 (4)
(4)
 (6)
(6)
 [
[ (x-1)-3]=2x-5,
(x-1)-3]=2x-5, ,
,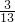 .
. ,
, +2x=2,
+2x=2, .
. ,
,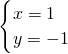 ;
; ,
, y=-1两边同乘以9,得
y=-1两边同乘以9,得 .
. y=-1两边同乘以9,然后与另一个方程相减消去y,解得x,再将x的值代入,即可解得y.
y=-1两边同乘以9,然后与另一个方程相减消去y,解得x,再将x的值代入,即可解得y.

 阅读快车系列答案
阅读快车系列答案