
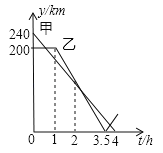
【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发![]() h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
【答案】②③④.
【解析】解:①观察函数图象可知,当t=2时,两函数图象相交,∵C地位于A、B两地之间,∴交点代表了两车离C地的距离相等,并不是两车相遇,结论①错误;
②甲车的速度为240÷4=60(km/h),乙车的速度为200÷(3.5﹣1)=80(km/h),∵(240+200﹣60﹣170)÷(60+80)=1.5(h),∴乙车出发1.5h时,两车相距170km,结论②正确;
③∵(240+200﹣60)÷(60+80)=![]() (h),∴乙车出发
(h),∴乙车出发![]() h时,两车相遇,结论③正确;
h时,两车相遇,结论③正确;
④∵80×(4﹣3.5)=40(km),∴甲车到达C地时,两车相距40km,结论④正确.
综上所述,正确的结论有:②③④.
故答案为:②③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一把直角三角尺的直角顶点放在点
,将一把直角三角尺的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,其中
的下方,其中![]() .
.

(1)将图1中的三角尺绕点![]() 顺时针旋转至图2,使一边
顺时针旋转至图2,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,求
,求![]() 的度数;
的度数;
(2)将图1中三角尺绕点![]() 按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边
按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边![]() 恰好与射线
恰好与射线![]() 平行;在第 秒时,直线
平行;在第 秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() .
.
(3)将图1中的三角尺绕点![]() 顺时针旋转至图3,使
顺时针旋转至图3,使![]() 在
在![]() 的内部,请探究
的内部,请探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,它与坐标轴分别交于A,B两点.
,它与坐标轴分别交于A,B两点.
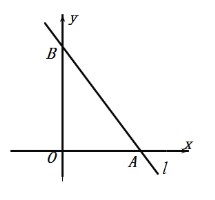
(1)求出点A的坐标;
(2)动点C从y轴上的点![]() 出发,以每秒1个单位长度的速度向y轴负半轴运动,求出点C运动的时间t,使得
出发,以每秒1个单位长度的速度向y轴负半轴运动,求出点C运动的时间t,使得![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的新机器可选,其中每台的价格、工作量如下表.
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多2万元,购买2台甲型机器比购买3台乙型机器少6万元.
(1)求a、b的值;
(2)若该公司购买新机器的资金不能超过110万元,请问该公司有几种购买方案?
(3)在(2)的条件下,若公司要求每月的产量不低于2040吨,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com