
����Ŀ����ͼ1����![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬����
��һ�㣬����![]() ������
������![]() ��ʹ
��ʹ![]() ����һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�
����һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�![]() ����һ��
����һ��![]() ������
������![]() �ϣ���һ��
�ϣ���һ��![]() ��ֱ��
��ֱ��![]() ���·�������
���·�������![]() .
.

��1����ͼ1�е����dz��Ƶ�![]() ˳ʱ����ת��ͼ2��ʹһ��
˳ʱ����ת��ͼ2��ʹһ��![]() ��
��![]() ���ڲ�����ǡ��ƽ��
���ڲ�����ǡ��ƽ��![]() ����
����![]() �Ķ���;
�Ķ���;
��2����ͼ1�����dz��Ƶ�![]() ��ÿ��10���ٶ���˳ʱ�뷽����תһ�ܣ���ת�����У��ڵ� ��ʱ����
��ÿ��10���ٶ���˳ʱ�뷽����תһ�ܣ���ת�����У��ڵ� ��ʱ����![]() ǡ��������
ǡ��������![]() ƽ��;�ڵ� ��ʱ��ֱ��
ƽ��;�ڵ� ��ʱ��ֱ��![]() ǡ��ƽ�����
ǡ��ƽ�����![]() .
.
��3����ͼ1�е����dz��Ƶ�![]() ˳ʱ����ת��ͼ3��ʹ
˳ʱ����ת��ͼ3��ʹ![]() ��
��![]() ���ڲ�����̽��
���ڲ�����̽��![]() ��
��![]() ֮���������ϵ����˵������.
֮���������ϵ����˵������.
���𰸡�(1) 150��;(2) 9��27��6��24 ;(3)������.
��������
��1�����ݽ�ƽ���ߵĶ��������COM��Ȼ����ݡ�CON=��COM+90����𣻣�2���ֱ�������������ƽ���ߵ����ʺ���ת�����������ת�ǣ�Ȼ�������ת�ٶȼ��ɵý⣻
��3���á�BOM�͡�NOC��ʾ����BON��Ȼ���г������������ɵý⣮
�⣺��1����OMƽ�֡�AOC��
���COM=![]() ��AOC=60����
��AOC=60����
���CON=��COM+90��=150����
��2�����ߡ�AOC=120����
���BOC=60����
�ߡ�OMN=30����
�൱ON��ֱ��AB��ʱ��MN��OC��
��ת��Ϊ90����270����
��ÿ��˳ʱ����ת10����
��ʱ��Ϊ9��27��
ֱ��ONǡ��ƽ����ǡ�BOCʱ��
��ת��Ϊ60���� 180��+60��=240����
��ÿ��˳ʱ����ת10����
��ʱ��Ϊ6��24��
�ʴ�Ϊ��9��27��6��24��
��3���ߡ�MON=90������BOC=60����
���BON=90��-��BOM��
��BON=60��-��NOC��
��90��-��BOM=60��-��NOC��
���BOM-��NOC=30����
�ʡ�BOM���NOC֮���������ϵΪ����BOM-��NOC=30����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������й��Ŵ���ѧר��������ѧ����������ijɾͣ����������ᵽ�˷������⣬Ҳ���ȼ�¼�ˡ�ӯ���㡱�����⣮����һ��������ӯ���㡱�����⣬ԭ�����£����й����˳��ţ�ӯʮһ���˳���������ʮ���������������۸����Σ�����Ϊ�����������˺ϻ��Ǯ�����ÿ�˳�9��Ǯ���ͻ��11��Ǯ�����ÿ�˳�6��Ǯ���ֻ�ȱ16��Ǯ���������������ļ۸���Ƕ��٣������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ʒ�̵��ϰ嵽�����̳�����������������![]() ������֪�������̳�������������ƽ��ÿ��
������֪�������̳�������������ƽ��ÿ��![]() Ԫ�����������ÿ����
Ԫ�����������ÿ����![]() Ԫ�����������ÿ����
Ԫ�����������ÿ����![]() Ԫ.
Ԫ.
��1�� �����������ÿ��������Ԫ��
��2�� �����������ϰ�����������������������ֹ�![]() ������������1060Ԫ���ʸ��ϰ�������������������˼�����
������������1060Ԫ���ʸ��ϰ�������������������˼�����
��3�� ���ϰ���㽫ÿһ��������![]() Ԫ���ٽ��д������ۣ��������������ۣ����������ۣ��ڣ�2��������£�Ϊ������������������һ���������������˼��������㲢˵������.
Ԫ���ٽ��д������ۣ��������������ۣ����������ۣ��ڣ�2��������£�Ϊ������������������һ���������������˼��������㲢˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
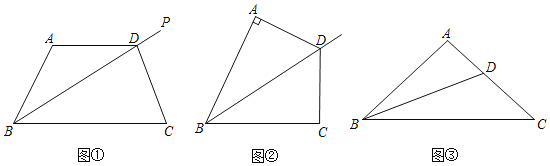
����Ŀ�������⣩��ͼ�٣���D�ǡ�ABC�Ľ�ƽ����BP��һ�㣬����AD��CD������A���C���������߶�AD��CD��ʲô������ϵ��
��̽����
̽��һ����ͼ�ڣ�����A��90�������C��180������A��90������AD��AB��CD��BC������ΪBDƽ�֡�ABC������AD��CD�������ǣ��� ����
̽����������A��90���������ͼ�٣�̽��AD��CD��������ϵ��˵�����ɣ�
[����]��D�ǡ�ABC�Ľ�ƽ����BP��һ�㣬����AD��CD������A���C���������߶�AD��CD��������ϵ���� ����
[��չ]��֪����ͼ�ۣ�����ABC�У�AB��AC����A��100����BDƽ�֡�ABC��
��֤��BC��AD+BD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ,��
,��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]()
��1����ͼ1����![]() ����
����![]() (ֱ��д�����) .
(ֱ��д�����) .
��2����ͼ2����![]() Ϊ
Ϊ![]() �ĵ㣬����
�ĵ㣬����![]() ,��
,��![]() ��ֵ;
��ֵ;
��3����ͼ3,��![]() ����
����![]() ,��
,��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
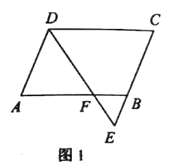
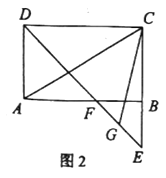
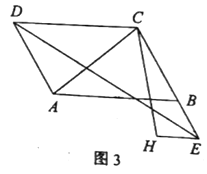
����Ŀ��������ABCD�ڽ��ڡ�O����ͼ��ʾ�����ӻ�![]() ��ȡһ��E������DE��BE������D��DF��BE����O�ڵ�F������BF��AF����AF��DE�ཻ�ڵ�G����֤��
��ȡһ��E������DE��BE������D��DF��BE����O�ڵ�F������BF��AF����AF��DE�ཻ�ڵ�G����֤��

��1���ı���EBFD�Ǿ��Σ�
��2��DG=BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и�ʽ�����ȫƽ��ʽ:
��x2+6x+______=��x+____��2 ��x2��5x+_____=��x��____��2��
��x2+ x+______=��x+____��2 ��x2��9x+_____=��x��____��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ÿ������9ʱ�����г��뿪�ң�15ʱ�ؼң����������ҵľ���ʱ��ı仯�����

��1��ͼ���ʾ�����������Ĺ�ϵ���ĸ����Ա������ĸ����������
��2��10ʱ��13ʱ�����ֱ���Ҷ�Զ��
��3�������������Զ�ĵط�ʱʲôʱ�䣿��Ҷ�Զ��
��4��11ʱ��12ʱ����ʻ�˶���ǧ�ף�
��5�����������Զ�ĵط����ص�ƽ���ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
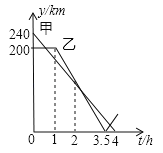
����Ŀ����һ����ֱ�Ĺ�·����A��B��C���أ�C��λ��A��B����֮�䣬�׳���A����������·����ʻ��C�أ��ҳ���B����������·����ʻ��A�أ��ڼ׳��������׳�����C�صĹ����У��ס�������������C�صľ���y��km����׳���ʻʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ�����н��ۣ��ټ׳�����2hʱ���������������ҳ�����1.5hʱ���������170km�����ҳ�����![]() hʱ�������������ܼ׳�����C��ʱ���������40km��������ȷ����______����д������ȷ���۵���ţ���
hʱ�������������ܼ׳�����C��ʱ���������40km��������ȷ����______����д������ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com