Question

【题目】在中，的平分线交于点,交的延长线于点

（1）如图1，若，则 (直接写出结果) .

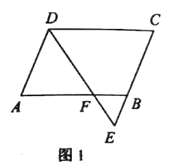
（2）如图2，若为的点，连接,求的值;

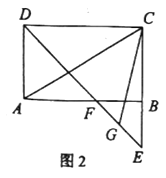
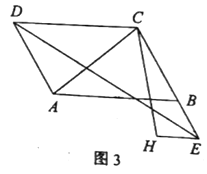
（3）如图3,若连接,求的值.

Answer 1

【答案】（1）3 （2） （3）1

【解析】

（1）由角平分线的定义和等腰三角形的判定与性质可得出AD＝AF＝2，BE＝BF＝1，则CD的长可求出；

（2）连接AG，BG，证明△AFG≌△CBG（SAS），可得AG＝CG，∠AGF＝∠CGB，则∠AGC＝∠FGB＝90°，可求出答案；

（3）分别延长DA，EH交于点N，连接CN，证明四边形DNEC是菱形，可得出△DCN和△CEN都是等边三角形，则CN＝CE，∠DNC＝∠NEC＝60°，证明△ANC≌△HEC（SAS），得出AC＝HC，则答案求出．

（1）如图

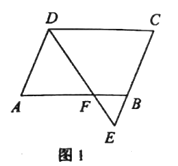
∵四边形ABCD为平行四边形，

∴DC∥AB，AD∥BC，

∴∠CDF＝∠DFA，

∵∠ADC的平分线交AB于点F，

∴∠CDF＝∠ADF，

∴∠ADF＝∠DFA，

∴AD＝AF＝2，

∵AD∥BC，

∴∠E＝∠ADF，

∵∠AFD＝∠BFE，

∴∠BFE＝∠E，

∴BE＝BF＝1．

∴AB＝DC＝2＋1＝3．

故答案为：3．

（2）如图，连接AG，BG．

∵四边形ABCD为平行四边形，∠ADC＝90°，

∴四边形ABCD为矩形，

∴∠ABC＝90°，

∴∠EBF＝90°，

∵G为EF的中点，

∴FG＝BG＝EG，

∴∠BFG＝∠FBG＝45°，

∴∠AFG＝∠CBG＝135°，

∵∠AFD＝∠BFG，

∴∠AFD＝45°，

∴AD＝AF，

∵AD＝BC，

∴BC＝AF，

∴△AFG≌△CBG（SAS），

∴AG＝CG，∠AGF＝∠CGB，

∴∠AGC＝∠FGB＝90°，

∴AC＝=CG，

∴；

（3）如图，分别延长DA，EH交于点N，连接CN，

∵∠ADC＝60°，DE平分∠ADC，

∴∠DCE＝120°，∠CDE＝30°，

∴∠CED＝30°，

∴∠CDE＝∠CED，

∴CD＝CE，

∵EH∥AB，AB∥CD，

∴EN∥CD，

∵DN∥CE，

∴四边形DNEC为平行四边形，

∴四边形DNEC是菱形，

∴DC＝DN，

∵∠ADC＝60°，

∴△DCN和△CEN都是等边三角形，

∴CN＝CE，∠DNC＝∠NE＝60°，

∵EH＝BE，

∴AN＝BE＝EH，

∴△ANC≌△HEC（SAS），

∴AC＝HC，

∴＝1．