
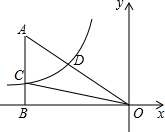
 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18. 分析 由点D为线段OA的中点可得出D点的坐标,将点D的坐标代入双曲线解析式中解出k值,即可得出双曲线的解析式,再令x=-8可得点C的坐标,根据边与边的关系结合三角形的面积公式即可得出结论.
解答 解:∵点D为线段OA的中点,且点A的坐标为(-8,6),
∴点D的坐标为(-4,3).
将点D(-4,3)代入到y=$\frac{k}{x}$中得:
3=$\frac{k}{-4}$,解得:k=-12.
∴双曲线的解析式为y=-$\frac{12}{x}$.
令x=-8,则有y=-$\frac{12}{-8}$=$\frac{3}{2}$,
即点C的坐标为(-8,$\frac{3}{2}$).
∵AB⊥BD,
∴点B(-8,0),AC=6-$\frac{3}{2}$=$\frac{9}{2}$,OB=0-(-8)=8,
∴△AOC的面积S=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×$\frac{9}{2}$×8=18.
故答案为:18.
点评 本题考查了反比例函数系数k的几何意义、中点坐标公式以及三角形的面积公式,解题的关键是找出点C、D的坐标.解决该题型题目时,求出点的坐标由待定系数法求出反比例函数解析式是关键.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
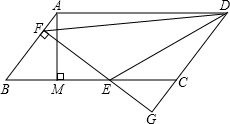 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2015 | D. | -2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
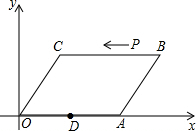 如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s
如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s查看答案和解析>>
科目:初中数学 来源: 题型:解答题
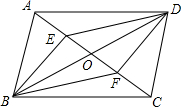 如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.
如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
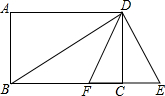 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+y2-8y的值为( )
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+y2-8y的值为( )| A. | 16 | B. | 15 | C. | 13 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com