
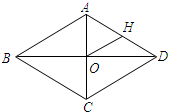
 如图,在菱形ABCD中,对角线AC、BD相交于点O、H为边AD的中点,菱形的周长为48,则OH的长是6.
如图,在菱形ABCD中,对角线AC、BD相交于点O、H为边AD的中点,菱形的周长为48,则OH的长是6.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
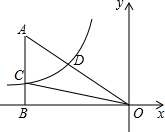 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
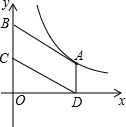 如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
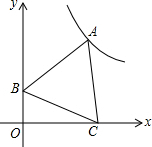 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )| A. | (3$\sqrt{3}$,4) | B. | (4,3$\sqrt{3}$) | C. | (4$\sqrt{3}$,3) | D. | (3,4$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
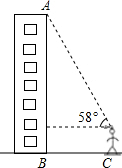 小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)
小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
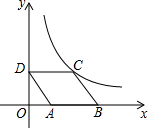 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
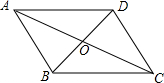 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )| A. | DC=BC | B. | AC⊥BD | C. | AB=BD | D. | ∠ADB=∠CDB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
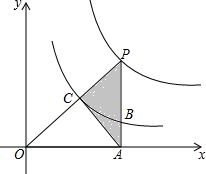 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
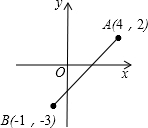 如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com