
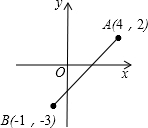
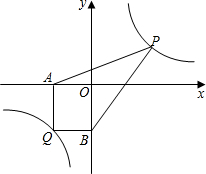
 如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标. 分析 如图,当AB为边,①当四边形ABQ2P2是平行四边形,所以AB=P2Q2,AP2=BQ2,②当四边形QPBA是平行四边形,所以AB=PQ,QA=PB,③当AB为对角线,即当四边形P1AQ1B是平行四边形,所以AP1=Q1B,AQ1=BP1,结合图形分别得出即可.
解答 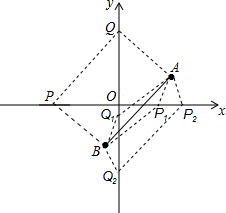 解:如图所示,
解:如图所示,
当AB为边,①即当四边形ABQ2P2是平行四边形,所以AB=P2Q2,AP2=BQ2,
∵点A(4,2),B(-1,-3),
∴AB=5$\sqrt{2}$,则OP2=OQ2=5,
∴Q2点的坐标是:(0,-5),
②当四边形QPBA是平行四边形,所以AB=PQ,QA=PB,
∴Q点的坐标是:(0,5),
③当AB为对角线,即当四边形P1AQ1B是平行四边形,
所以AP1=Q1B,AQ1=BP1,
∴Q1点的坐标是:(0,-1).
综上所述:符合题意的点Q的坐标为:(0,-5)或(0,-1)或(0,5).
点评 此题考查了平行四边形的性质:平行四边形的对边平行且相等,结合AB的长分别确定P,Q的位置是解决问题的关键.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
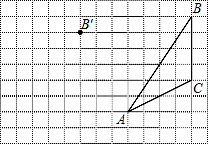 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
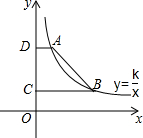 如图,点A(2,6),B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=4.
如图,点A(2,6),B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 【阅读理解】对于任意正实数a、b,
【阅读理解】对于任意正实数a、b,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com