
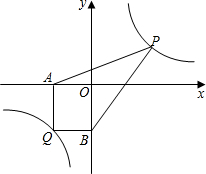
 【阅读理解】对于任意正实数a、b,
【阅读理解】对于任意正实数a、b,分析 (1)根据阅材料可得,当m=$\frac{4}{m}$时,m+$\frac{4}{m}$取得最大值,据此即可求解;
(2)连接PQ,设P(x,$\frac{12}{x}$),根据根据四边形AQBP的面积=△AQP的面积+△QBP的面积,从而利用x表示出四边形的面积,利用阅读材料中介绍的不等式的性质即可求解.
解答 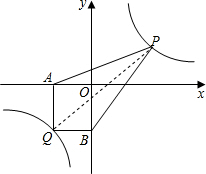 解:(1)根据题意得当m=$\frac{4}{m}$时,m=2,此时m+$\frac{4}{m}$=4.
解:(1)根据题意得当m=$\frac{4}{m}$时,m=2,此时m+$\frac{4}{m}$=4.
故答案是:2,4;
(2)连接PQ,设P(x,$\frac{12}{x}$),
∴S四边形AQBP=$\frac{1}{2}$×4(x+3)+$\frac{1}{2}$×3($\frac{12}{x}$+4)
=2x+$\frac{18}{x}$+12≥12+12=24.
∴最小值为24.
点评 本题考查了反比例函数的性质以及不等式的性质,正确读懂已知中的不等式的性质,表示出四边形AQBP的面积是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
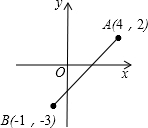 如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | ±3 | C. | 6 | D. | ±6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm,6cm | B. | 6cm,8cm | C. | 8cm,12cm | D. | 20cm,30cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{{x}^{2}}+\frac{1}{x}-3=0$ | B. | ax2+bx+c=0 | C. | x2+5x=x2-3 | D. | x2-3x+2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.00129 | B. | 0.0129 | C. | -0.00129 | D. | 0.000129 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
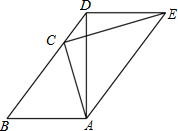 如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com