Question

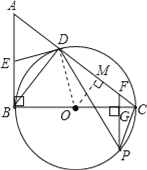
【题目】如图，已知AB是⊙O的切线，BC为⊙O的直径，AC与⊙O交于点D，点E为AB的中点，PF⊥BC交BC于点G，交AC于点F

（1）求证：ED是⊙O的切线；

（2）求证：△CFP∽△CPD；

（3）如果CF=1，CP=2，sinA=，求O到DC的距离．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）O到DC的距离为．

【解析】试题分析：（1）连接OD，证OD⊥DE即可．易证∠ADB=90°，又点E为AB的中点，得DE=EB．根据等腰三角形性质可证∠ODE=∠OBE=90°，得证；

（2）可证∠A=∠DBC，所以要求BC需先求DC．结合已知条件，证明△PDC与△FPC相似．

（3）根据△PCF∽△DCP，得出CD的长度，进而求出O到DC的距离即可．

试题解析：（1）连接OD．

∵BC为直径，

∴△BDC为直角三角形．

在Rt△ADB中，E为AB中点，

∴BE=DE，

∴∠EBD=∠EDB．

又∵OB=OD，∴∠OBD=∠ODB，

∵∠OBD+∠ABD=90°，∴∠ODB+∠EDB=90°．

∴ED是⊙O的切线．

（2）∵PF⊥BC，

∴∠FPC=90°﹣∠BCP（直角三角形的两个锐角互余）．

∵∠PDC=90°﹣∠PDB（直径所对的圆周角是直角），∠PDB=∠BCP（同弧所对的圆周角相等），

∴∠FPC=∠PDC（等量代换）．

又∵∠PCF是公共角，

∴△PCF∽△DCP．

（3）过点O作OM⊥CD于点M，

∵△PCF∽△DCP，

∴PC2=CFCD（相似三角形的对应边成比例）．

∵CF=1，CP=2，

∴CD=4．

可知sin∠DBC=sinA=sin∠MOC=，

∴=，即=，

∴直径BC=5，

∴=，

∴MC=2，

∴MO=，

∴O到DC的距离为．