
如图,矩形ABCD的对角线AC,BD交于点O, DE∥AC交BA的延长线于点E,点F在BC上,BF=BO,且AE=6,AD=8.
(1)求BF的长;
(2)求四边形OFCD的面积.

(1)BF=5;(2)
【解析】
试题分析:(1)在Rt△EAD中,利用勾股定理求得DE=10;然后利用?ACDE的对边相等得到:AC=DE=10;最后在Rt△ABC中根据“直角三角形斜边上的中线等于斜边的一半”和已知条件来求BF=BO=5;
(2)过点O作OG⊥BC于点G.由图形得到 .利用三角形中位线定理得到OG是△BCD的中位线.利用(1)中平行四边形ACDE的性质求得相关线段的长度,将其代入进行计算即可.
.利用三角形中位线定理得到OG是△BCD的中位线.利用(1)中平行四边形ACDE的性质求得相关线段的长度,将其代入进行计算即可.
试题解析:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠EAD=180°﹣∠BAD=90°.
∵在Rt△EAD中,AE=6,AD=8,
∴ .
.
∵DE∥AC,AB∥CD,
∴四边形ACDE是平行四边形.
∴AC=DE=10.
在Rt△ABC中,∠ABC=90°,
∵OA=OC,
∴ .
.
∵BF=BO,
∴BF=5.
(2)过点O作OG⊥BC于点G.
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴CD⊥BC.
∴OG∥CD.
∵OB=OD,∴BG=CG,
∴OG是△BCD的中位线.
由(1)知,四边形ACDE是平行四边形,AE=6,
∴CD=AE=6.
∴ .
.
∵AD=8,
∴BC=AD=8.
∴ ,
, .
.
∴ .
.

考点:1.矩形的性质;2.勾股定理;3.三角形中位线定理;4.平行四边形的判定与性质


科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:填空题
如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
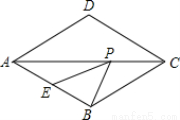
查看答案和解析>>
科目:初中数学 来源:2015届北京市房山区八年级下学期期末考试数学试卷(解析版) 题型:选择题
在平面直角坐标中,点P(﹣3,5)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:选择题
一个多边形有9条对角线,则这个多边形有多少条边( )
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源:2015届北京市丰台区八年级下学期期末考试数学试卷(解析版) 题型:解答题
已知一次函数 的图象与
的图象与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .
.
(1)求 ,
, 两点的坐标;
两点的坐标;
(2)过 点作直线
点作直线 P与x轴交于点
P与x轴交于点 ,且使△A
,且使△A P的面积为2,求点P的坐标.
P的面积为2,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作
中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作 .
.
(1)已知⊙O是以原点为圆心,1为半径的圆,点P(0,2),
①直线 :
: ,直线
,直线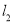 :
: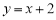 ,直线
,直线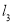 :
: ,直线
,直线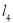 :
: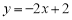 都经过点P,在直线
都经过点P,在直线 ,
, 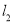 ,
, 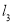 ,
, 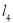 中,是⊙O的“x关联直线”的是 ;
中,是⊙O的“x关联直线”的是 ;
②若直线 是⊙O的“x关联直线”,则点M的横坐标
是⊙O的“x关联直线”,则点M的横坐标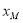 的最大值是 ;
的最大值是 ;
(2)点A(2,0),⊙A的半径为1,
①若P(-1,2),⊙A的“x关联直线” :
: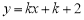 ,点M的横坐标为
,点M的横坐标为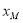 ,当
,当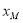 最大时,求k的值;
最大时,求k的值;
②若P是y轴上一个动点,且点P的纵坐标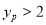 ,⊙A的两条“x关联直线”
,⊙A的两条“x关联直线” ,
, 是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com