
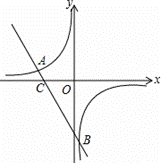
如图所示,直线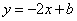 与反比例函数
与反比例函数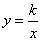 交于点
交于点
A、B,与x轴交于点C.
(1)若A(-3,m)、B(1,n).
直接写出不等式 的解;
的解;
(2)求sin∠OCB的值.
科目:初中数学 来源: 题型:
商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
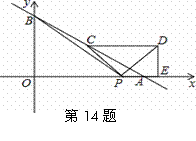
如图:直线 与x,y轴分别交于A,B,C
与x,y轴分别交于A,B,C
是AB的中点,点P从A出发以每秒1个单位的速度沿
射线AO方向运动,将点C绕P顺时针旋转90°得到
点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设
点P的运动时间为t秒(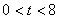 ),当以P,D,E为
),当以P,D,E为
顶点的三角形与△BOP相似时,写出所有t的值 ;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线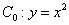 ,顶点记作
,顶点记作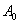 .首先我们将抛物线
.首先我们将抛物线 关于直线
关于直线 对称翻折过去得到抛物线
对称翻折过去得到抛物线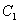 称为第一次操作,再将抛物线
称为第一次操作,再将抛物线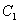 关于直线
关于直线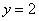 对称翻折过去得到抛物线
对称翻折过去得到抛物线 称为第二次操作,…,将抛物线
称为第二次操作,…,将抛物线 关于直线
关于直线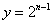 对称翻折过去得到抛物线
对称翻折过去得到抛物线 (顶点记作
(顶点记作 )称为第n此操作(n=1,2,3…),….设抛物线
)称为第n此操作(n=1,2,3…),….设抛物线 与抛物线
与抛物线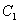 交于两点
交于两点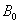 与
与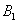 ,顺次连接
,顺次连接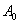 、
、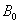 、
、 、
、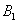 四个点得到四边形
四个点得到四边形 ,抛物线
,抛物线 与抛物线
与抛物线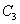 交于两点
交于两点 与
与 ,顺次连接
,顺次连接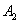 、
、 、
、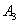 、
、 四个点得到四边形
四个点得到四边形 ,…,抛物线
,…,抛物线 与抛物线
与抛物线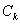 交于两点
交于两点 与
与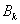 ,顺次连接
,顺次连接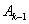 、
、 、
、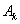 、
、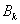 四个点得到四边形
四个点得到四边形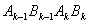 (k=1,3,5…),….
(k=1,3,5…),….
(1)请分别直接写出抛物线 (n=1,2,3,4)的解析式;
(n=1,2,3,4)的解析式;
 (2)一系列四边形
(2)一系列四边形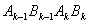 (k=1,3,5…)
(k=1,3,5…)
为哪种特殊的四边形(说明理由)?它们
都相似吗?如果全都相似,请证明之;如
果不全都相似,请举出一对不相似的反例;
(3)试归纳出抛物线 的解析式,无需证明.
的解析式,无需证明.
并利用你归纳出来的 的解析式
的解析式
求四边形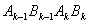 (k=1,3,5…)
(k=1,3,5…)
的面积(用含k的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com