已知△ABC和△DEF相似，且△ABC的三边长为3、4、5，如果△DEF的周长为6，那么下列不可能是△DEF一边长的是（ ）
A． 1.5 B． 2 C． 2.5 D． 3．
D
考点： 相似三角形的性质．
分析： 由△ABC的三边长为2、3、4，即可求得△ABC的周长，然后根据相似三角形周长的比等于相似比得出两三角形的相似比，再把各选项中的值与相似比相乘即可得出结论．
解答： 解：∵△ABC的三边长为3、4、5，
∴△ABC的周长=12，
∴
=
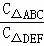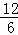=2，
A、1.5×2=3，与△ABC一边长相符，故本选项正确；
B、2×2=4，与△ABC一边长相符，故本选项正确；
C、2.5×2=5，与△ABC一边长相符，故本选项正确；
D、3×2=6，故本选项错误．
故选D．
点评： 本题考查的是相似三角形的性质，熟知相似三角形周长的比等于相似比是解答此题的关键．
科目：初中数学 来源： 题型：
△ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1：2，已知△A
BC的面积是3，则△A′B′C′的面积是( )
A．3 B．6 C．9 D．12
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读材料：
例：说明代数式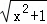
+
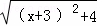的几何意义，并求它的最小值．
解：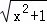
+
=
+
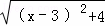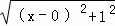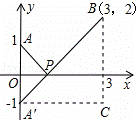
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则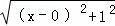
可以看成点P与点A（0，1）的距离，
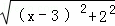可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．
设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B=3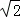
，即原式的最小值为3．
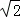根据以上阅读材料，解答下列问题：
（1）代数式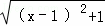
+
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B（2，3）或（2，﹣3）的距离之和．（填写点B的坐标）
（2）代数式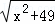
+
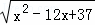的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
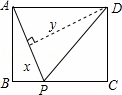
如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是( )
A．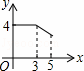
B．
C．
D．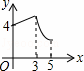
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
）﹣2×（﹣600）0﹣（﹣3）3×0.1﹣1×π0