
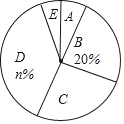
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 | m | 54 | 9 |
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %.
(2)被调查学生的总人数为 人,统计表中m的值为 ,统计图中n的值为 ;
(3)在统计图中,B类所对应扇形圆心角的度数为 ;
(4)该校共有1000名学生,根据调查结果,估计该校最喜爱A类节目的人数.
【答案】(1)30,20;(2)150,45,36;(3)72°;(4)估计该校最喜爱A类节目的学生数为80人
【解析】
(1)观察图表体育类型即可解决问题;(2)根据“总数=B类型的人数÷B所占百分比”可得总数;用总数减去其他类型的人数,可得m的值;根据百分比=所占人数/总人数可得n的值;(3)根据圆心角度数=360°×所占百分比,计算即可;(4)用学生数乘以最喜爱新闻节目所占百分比可估计最喜爱新闻节目的学生数.
(1)最喜爱体育节目的有30人,这些学生数占被调查总人数的百分比为20%.
故答案为30,20.
(2)总人数=30÷20%=150人,
m=150﹣12﹣30﹣54﹣9=45,
n%=![]() ×100%=36%,即n=36,
×100%=36%,即n=36,
故答案为:150,45,36.
(3)B类所对应扇形圆心角的度数为360°×20%=72°.
故答案为:72°
(4)估计该校最喜爱A类节目的学生数为1000×![]() =80人.
=80人.
答:估计该校最喜爱A类节目的学生数为80人.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的过程中,利用 法(把未知数x换为 y)达到降次的目的.
(2)解方程:(x2+3x)2+5(x2+3x)-6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
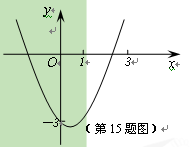
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
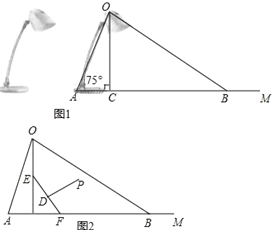
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.73)
≈1.73)
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.试问:最佳视点P在不在灯光照射范围内?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.
的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.

查看答案和解析>>
科目:初中数学 来源: 题型:
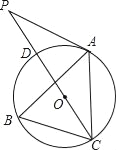
【题目】如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.则PD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
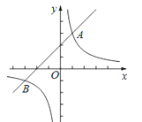
【题目】如图,一次函数y=x+2的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 为反比例函数.
为反比例函数.
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)求出﹣2≤x≤﹣![]() 时,y的取值范围.
时,y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com