练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

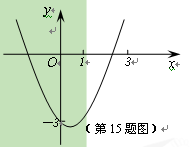
    【题目】（11·湖州）如图，已知抛物线经过点（0，－3），请你确定一个

    b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间。你确定的b的值是 ▲ 。

    【答案】如（答案不唯一）

    【解析】把（0，-3）代入抛物线的解析式求出c的值，在（1，0）和（3，0）之间取一个点，分别把x=1和x=3它的坐标代入解析式即可得出不等式组，求出答案即可．

    解：把（0，-3）代入抛物线的解析式得：c=-3，
    ∴y=x2+bx-3，
    ∵使该抛物线与x轴的一个交点在（1，0）和（3，0）之间，
    ∴把x=1代入y=x2+bx-3得：y=1+b-3＜0
    把x=3代入y=x2+bx-3得：y=9+3b-3＞0，
    ∴-2＜b＜2，
    即在-2＜b＜2范围内的任何一个数都符合，
    故答案为：在-2＜b＜2范围内的任何一个数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】垫球是排球队常规训练的重要项目之一，下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩，测试规则为每次连续接球10个，每垫球到位1个记1分，已知运动员甲测试成绩的中位数和众数都是7．

    运动员甲测试成绩统计表

    测试序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    成绩（分）

    7

    6

    8

    7

    6

    8

    6

    8

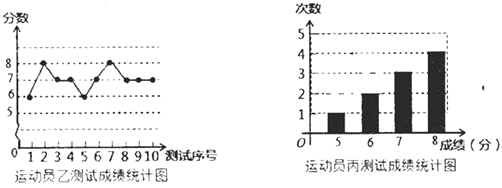
    （1）填空：______；______．

    （2）要从他们三人中选择一位垫球较为稳定的接球能手，你认为选谁更合适？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，菱形ABCD中，∠A=60°，点P从A出发，以2cm/s的速度沿边AB、BC、CD匀速运动到D终止，点Q从A与P同时出发，沿边AD匀速运动到D终止，设点P运动的时间为t（s）．△APQ的面积S（cm2）与t（s）之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出．

    （1）求点Q运动的速度；

    （2）求图2中线段FG的函数关系式；

    （3）问：是否存在这样的t，使PQ将菱形ABCD的面积恰好分成1：5的两部分？若存在，求出这样的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC

    ①求证：△ABE≌△CBD；

    ②若∠CAE=30°，求∠BDC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=-x2+bx+c与x轴交于点A(-1.0)和点B(3,0) ,与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点.

    (1)求此抛物线的解析式

    (2)直接写出点C和点D的坐标

    (3)若点P在第一象限内的抛物线上,且S△ABP=4S△CDE，求P点坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

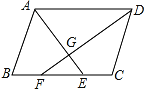
    【题目】如图，在ABCD中，∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F，AE与DF相交于点G.

    (1)求证：∠AGD=90°.

    (2) 求证：BF=CE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解方程

    （1）2x2﹣5x﹣3＝0

    （2）（2x﹣5）2＝4（2x﹣5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+x+4的对称轴是直线x=3，且与轴相交于A、B两点（B点在A点的右侧），与轴交于C点．

    （1）A点的坐标是　 　；B点坐标是　 　；

    （2）直线BC的解析式是：　 　；

    （3）点P是直线BC上方的抛物线上的一动点（不与B、C重合），是否存在点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积，若不存在，试说明理由；

    （4）若点M在x轴上，点N在抛物线上，以A、C、M、N为顶点的四边形是平行四边形时，请直接写出点M点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，∠A＝90°，BD是∠ABC的平分线，DE⊥BC于E，若BC＝12，则△DEC的周长为_____．

    查看答案和解析>>

    同步练习册答案