
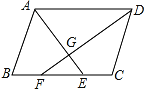
【题目】如图,在ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
(1)求证:∠AGD=90°.
(2) 求证:BF=CE.
【答案】(1)见详解;(2)见详解
【解析】
(1)由平行四边形的性质和角平分线的定义即可得出结论;
(2)根据平行四边形的性质和平行线的性质推出∠ADF=∠CFD,结合∠ADF=∠CDF求出CD=CF,同理可得AB=BE,即可证明BF=CE.
解:(1)∵四边形ABCCD是平行四边形,
∴∠BAD+∠ADC=180°,
∵AE、DF分别是∠BAD、∠ADC的平分线,
∴∠DAG=![]() ∠BAD,∠ADG=
∠BAD,∠ADG=![]() ∠ADC,
∠ADC,
∴∠DAG+∠ADG=![]() ×(∠BAD+∠ADC)=
×(∠BAD+∠ADC)=![]() ×180°=90°,
×180°=90°,
∴∠AGD=90°;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CFD,
∵∠ADF=∠CDF,
∴∠CDF=∠CFD,
∴CD=CF
同理可得AB=BE,
∵AB=CD,
∴CF=BE,
∵BE=BF+EF,CF=CE+EF
∴BF=CE.


科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级二班![]() 名同学在“爱心捐款”活动中,捐款情况统计如表,
名同学在“爱心捐款”活动中,捐款情况统计如表,
捐款金额(元) |
|
|
|
|
|
捐款人数(人) |
|
|
|
|
|
![]() 表中
表中![]() ________;
________;
![]() 二班同学捐款数组成的数据中,中位数是________、众数是________;
二班同学捐款数组成的数据中,中位数是________、众数是________;
![]() 九年级二班
九年级二班![]() 名同学平均捐款多少元?
名同学平均捐款多少元?
![]() 根据样本数据,估计该校九年级
根据样本数据,估计该校九年级![]() 名学生在本次活动中捐款多于
名学生在本次活动中捐款多于![]() 元的人数.
元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有【 】个.

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
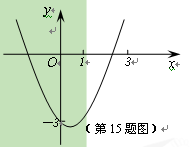
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论: ①c>0; ②4a-2b+c>0. ③2a-b=0;④若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1>y2; 其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N.
(1)求证:△AMC≌△CNB;
(2)求证:MN=AM+BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
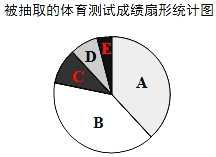
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com