
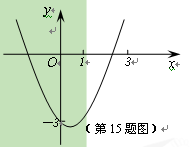
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)A点的坐标是 ;B点坐标是 ;
(2)直线BC的解析式是: ;
(3)点P是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积,若不存在,试说明理由;
(4)若点M在x轴上,点N在抛物线上,以A、C、M、N为顶点的四边形是平行四边形时,请直接写出点M点坐标.

【答案】(1)A(![]() ,0) B(8,0);(2)
,0) B(8,0);(2)![]() ; (3)存在点P,使△PBC的面积最大,最大面积是16 ;(4)(
; (3)存在点P,使△PBC的面积最大,最大面积是16 ;(4)(![]() ,0),(4, 0),(
,0),(4, 0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
![]() 可得a的值,求出解析式.由解析式可得出C和B的坐标,从而得出直线的解析式.运用假设法,连接辅助线可以设出P,D的坐标,表达出相应△PBC的面积解析式,分析可得出结果.由平行四边形的定义可求出答案.
可得a的值,求出解析式.由解析式可得出C和B的坐标,从而得出直线的解析式.运用假设法,连接辅助线可以设出P,D的坐标,表达出相应△PBC的面积解析式,分析可得出结果.由平行四边形的定义可求出答案.
(1)A(![]() ,0) B(8,0);
,0) B(8,0);
(2)![]() ;
;
(3)假设存在点P,连结PB、PC,过点P作PD∥y轴交直线BC于点D,
设点P(m,![]() )
)
则点D(m,![]() )
)
所以PD=![]()
![]()
=![]()
∴![]()
![]()
∵点P是直线BC上方的抛物线上的一动点(不与B、C重合)
∴![]()
∴当![]() 时,△PBC的面积最大,最大面积是16
时,△PBC的面积最大,最大面积是16
∴存在点P,使△PBC的面积最大,最大面积是16
(4)(![]() ,0),(4, 0),(
,0),(4, 0),(![]() ,0),(
,0),(![]() ,0) .
,0) .


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①x2-4x-1=0,②x(2x+1)=8x-3,③x2+3x+1=0,④x2-9=4(x-3)
我选择第几个方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生在同一小区居住,一天早晨,甲、乙两人同时从家出发去同一所学校上学.甲骑自行车匀速行驶.乙步行到公交站恰好乘上一辆公交车,公交车沿公路匀速行驶,公交车的速度分别是甲骑自行车速度和乙步行速度的2倍和5倍,下车后跑步赶到学校,两人同时到达学校(上、下车时间忽略不计).两人各自距家的路程y(m)与所用的时间x(min)之间的函数图象如图所示.
(1)a= ,b= .
(2)当乙学生乘公交车时,求y与x之间的函数关系式(不要求写出自变量x的取值范围).
(3)如果乙学生到学校与甲学生相差1分钟,直接写出他跑步的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N.
(1)求证:△AMC≌△CNB;
(2)求证:MN=AM+BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C = 90°,![]() .D为BC上一点,且到A,B两点的距离相等.
.D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B = 35°,求∠CAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,以
,以![]() 为直径,
为直径,![]() 为圆心的半圆交
为圆心的半圆交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的角平分线,且
的角平分线,且![]() ,垂足为点
,垂足为点![]() .
.
![]() 判断直线
判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com