
【题目】用适当的方法解方程
(1)2x2﹣5x﹣3=0
(2)(2x﹣5)2=4(2x﹣5)
【答案】(1)x1=3,x2=-![]() ;(2)x1=
;(2)x1=![]() ,x2=
,x2=![]() .
.
【解析】
(1)方程两边除以2将二次项系数化为1,常数项移到方程右边,然后左右两边都加上一次项系数一半的平方,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;
(2)根据因式分解法,可得答案.
解:(1)2x2-5x-3=0,
变形得:x2-![]() x=
x=![]() ,
,
配方得:x2-![]() x+
x+![]() =
=![]() +
+![]() ,即(x-
,即(x-![]() )2=
)2=![]() ,
,
开方得:x-![]() =±
=±![]() ,
,
则x1=3,x2=-![]() ;
;
(2)移项,得
(2x-5)2-4(2x-5)=0
因式分解,得
(2x-5)(2x-9)=0,
于是,得
2x-5=0或2x-9=0,
解得x1=![]() ,x2=
,x2=![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() (x>0),
(x>0),![]() (x>0),点P为双曲线
(x>0),点P为双曲线![]() 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别交双曲线![]() 于D、C两点,则△PCD的面积为( )
于D、C两点,则△PCD的面积为( )

A. 1 B. ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
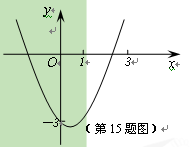
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生在同一小区居住,一天早晨,甲、乙两人同时从家出发去同一所学校上学.甲骑自行车匀速行驶.乙步行到公交站恰好乘上一辆公交车,公交车沿公路匀速行驶,公交车的速度分别是甲骑自行车速度和乙步行速度的2倍和5倍,下车后跑步赶到学校,两人同时到达学校(上、下车时间忽略不计).两人各自距家的路程y(m)与所用的时间x(min)之间的函数图象如图所示.
(1)a= ,b= .
(2)当乙学生乘公交车时,求y与x之间的函数关系式(不要求写出自变量x的取值范围).
(3)如果乙学生到学校与甲学生相差1分钟,直接写出他跑步的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C = 90°,![]() .D为BC上一点,且到A,B两点的距离相等.
.D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B = 35°,求∠CAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有一个△DEF.
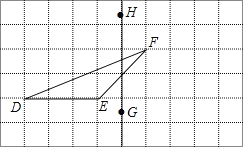
(1)画出△DEF关于直线HG的轴对称图形(不写画法);
(2)画EF边上的高(不写画法);
(3)若网格上的最小正方形边长为1,则△DEF的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com