
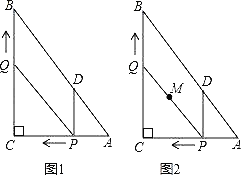
����Ŀ��С�ռҡ�������վ��ѧУ��һ����ֱ�Ĺ�·�ԣ�С�ռҡ�ѧУ��������·�ľ�����Բ��ƣ�һ�죬С�մӼҳ���ȥ��ѧ����������·���е�����վǡ�ó���һ������������������������·������ʻ��С���³�ʱ���ֻ���4�����ϿΣ�����������������·�ܲ��ϵ�ѧУ���ϡ��³�ʱ����Բ��ƣ���С����ѧУ�ľ���s����λ���ף��������õ�ʱ��t����λ�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ����֪С�մӼҳ���7����ʱ��ҵľ�����1200�ף����Ϲ�������������ѧУ����10���ӣ�����˵����
�ٹ��������ٶ�Ϊ400��/���ӣ�
��С�մӼҳ���5����ʱ���Ϲ�������
��С���¹�����������ѧУ���ٶ���100��/���ӣ�
��С���Ͽγٵ���1���ӣ�
������ȷ�ĸ����ǣ� ��
A.4��
B.3��
C.2��
D.1��
���𰸡�B
���������⣺��С�մӼҳ���7����ʱ��ҵľ�����1200�ף���С�մӼҳ���7����ʱ����ѧУ3500��1200=2300m��
��������ٶ�Ϊ�� ![]() =400��/���ӣ��ʢ���ȷ��
=400��/���ӣ��ʢ���ȷ��
�ɢ�֪�������ٶ�Ϊ400��/���ӣ�
�������ʻ��ʱ��Ϊ ![]() =7���ӣ�
=7���ӣ�
��С�մӼҳ������Ϲ��������ڵ�12��7=5����ʱ���ʢ���ȷ��
�ߴ��Ϲ�������������ѧУ����10���ӣ�
��С���¹�����������ѧУ���ٶ��� ![]() =100��/���ӣ��ʢ���ȷ��
=100��/���ӣ��ʢ���ȷ��
��С�մ��³�������ѧУ����ʱ��Ϊ5+10��12=3���ӣ�
��С���³�ʱ���ֻ���4�����ϿΣ�
��С���³����Ͽ���ǰ1���ӣ��ʢܴ���
��ѡ��B��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1���Ķ����⣺
���ǰ�����ij�����������е�����ɵ�ͼ�Σ�����������������ĵ�Ĺ켣��
���磺�ǵ�ƽ�����ǵ��ǵ����߾�����ȵĵ�Ĺ켣��
���⣺��ͼ1����֪EFΪ��ABC����λ�ߣ�M�DZ�BC��һ���㣬����AM��EF�ڵ�P����ô����PΪ�߶�AM�е㣮
���ɣ����߶�EFΪ��ABC����λ�ߣ���EF��BC��
��ƽ���߷��߶γɱ����ã�����PΪ�߶�AM�е㣮
�ɴ���õ�����P���˶��켣�ǣ� ��
��2��֪ʶӦ�ã�
��ͼ2����֪EFΪ�ȱߡ�ABC��AB��AC�ϵĶ��㣬����EF����AF=BE���ҵȱߡ�ABC�ı߳�Ϊ8�����߶�EF�е�Q���˶��켣�ij���
��3����չ��ߣ�
��ͼ3��PΪ�߶�AB��һ���㣨��P�����A��B�غϣ������߶�AB��ͬ��ֱ����ȱߡ�APC�͵ȱߡ�PBD������AD��BC������ΪQ��
�����AQB�Ķ�����
����AB=6����Q�˶��켣�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
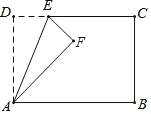
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=5��AB=8����EΪ����DC��һ�����㣬����ADE��ֱ��AE�۵�������D�Ķ�Ӧ��F�պ������߶�AB�Ĵ�ֱƽ������ʱ����DE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��ΪAB��AC��AB�ڵ�A��BC���O�ཻ�ڵ�D����AC��ȡһ��E��ʹ��ED=EA�� 
��1����֤��ED�ǡ�O�����ߣ�
��2����OE=10ʱ����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EΪABCD�ı�AB�ӳ����ϵ�һ�㣬��BE��AB=2��3����BEF�����Ϊ4����ABCD�����Ϊ�� �� 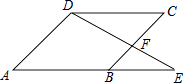
A.30
B.27
C.14
D.32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ���Rt��ABC��ֱ�DZ�AC��б��AB�������ȱߡ�ACD���ȱߡ�ABE����֪��ABC=60�㣬EF��AB������ΪF������DF�� 
��1����֤����ABC�ա�EAF��
��2�����ж��ı���EFDA����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��E��F�ֱ��ǡ�ABC�����е㣬��AB��AC��10��BC��12�����ı���ADEF���ܳ������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���һ������ֱ��������AOB����OAB=90�㣬ֱ�DZ�AO��x���ϣ���AO=1����Rt��AOB��ԭ��O˳ʱ����ת90��õ�����ֱ��������A1OB1����A1O=2AO���ٽ�Rt��A1OB1��ԭ��O˳ʱ����ת90��õ�����������A2OB2����A2O=2A1O�������˹��ɣ��õ�����ֱ��������A2017OB2017�����B2017������_______

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com