
【题目】已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.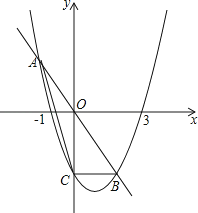
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为 ![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.
【答案】
(1)
解:令抛物线y=ax2+bx﹣3中x=0,则y=﹣3,
∴点C的坐标为(0,﹣3).
∵抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,
∴有 ![]() ,解得:
,解得: ![]() ,
,
∴此抛物线的解析式为y=x2﹣2x﹣3
(2)
解:将y=kx代入y=x2﹣2x﹣3中得:kx=x2﹣2x﹣3,
整理得:x2﹣(2+k)x﹣3=0,
∴xA+xB=2+k,xAxB=﹣3.
∵原点O为线段AB的中点,
∴xA+xB=2+k=0,
解得:k=﹣2.
当k=﹣2时,x2﹣(2+k)x﹣3=x2﹣3=0,
解得:xA=﹣ ![]() ,xB=
,xB= ![]() .
.
∴yA=﹣2xA=2 ![]() ,yB=﹣2xB=2
,yB=﹣2xB=2 ![]() .
.
故当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣ ![]() ,2
,2 ![]() ),点B的坐标为(
),点B的坐标为( ![]() ,﹣2
,﹣2 ![]() )
)
(3)
解:假设存在.
由(2)可知:xA+xB=2+k,xAxB=﹣3,
S△ABC= ![]() OC|xA﹣xB|=
OC|xA﹣xB|= ![]() ×3×
×3× ![]() =
= ![]() ,
,
∴(2+k)2﹣4×(﹣3)=10,即(2+k)2+2=0.
∵(2+k)2非负,无解.
故假设不成了.
所以不存在实数k使得△ABC的面积为 ![]()
【解析】(1)令抛物线解析式中x=0求出y值即可得出C点的坐标,有点(﹣1,0)、(3,0)利用待定系数法即可求出抛物线的解析式;(2)将正比例函数解析式代入抛物线解析式中,找出关于x的一元二次方程,根据根与系数的关系即可得出“xA+xB=2+k,xAxB=﹣3”,结合点O为线段AB的中点即可得出xA+xB=2+k=0,由此得出k的值,将k的值代入一元二次方程中求出xA、xB , 在代入一次函数解析式中即可得出点A、B的坐标;(3)假设存在,利用三角形的面积公式以及(2)中得到的“xA+xB=2+k,xAxB=﹣3”,即可得出关于k的一元二次方程,结合方程无解即可得出假设不成了,从而得出不存在满足题意的k值.本题考查了待定系数法求函数解析式、根与系数的关系、解一元二次方程以及三角形的面积公式,解题的关键是:(1)利用待定系数法求出函数解析式;(2)结合根与系数的关系求出k值;(3)利用反正法找出方程无解.本题属于中档题,难度不大,解决该题型题目时,将正比例函数解析式代入二次函数解析式中,利用三角形的面积公式结合根与系数的关系找出关于k的方程是关键.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:某商场因换季,将一品牌服装打折销售,每件服装如果按标价的六折出售将亏10元,而按标价的七五折出售将赚50元,问:
(1) 每件服装的标价是多少元?
(2) 每件服装的成本是多少元?
(3)为保证不亏本,最多能打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=![]() S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
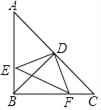
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.
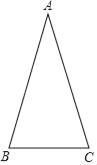
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个底面直径为 5cm,高为 18cm 的圆柱形瓶内装满水,再将瓶内得水倒入一个底面直径为 6cm,高为 10cm 的圆柱形玻璃杯中,能否完全装下? 若装不下,那么瓶内水面还有多高? 若未能装满,求杯内水面离杯口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.
(1)写出数轴上点A、C表示的数;
(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=![]() CQ.设运动的时间为t(t>0)秒.
CQ.设运动的时间为t(t>0)秒.
①数轴上点M、N表示的数分别是 (用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律,完成相关题目.
老师说:“我定义了一种新的运算,叫(加乘)运算.”
然后老师写出了一些按照(加乘)运算的运算法则进行运算的算式:
(+5)(+2)=+7;(-3)(-5)=+8;
(-3)(+4)=-7; (+5)(-6)=-11;
0(+8)=8;(-6)0=6.
小明看了这些算式后说:“我知道老师定义的(加乘)运算的运算法则了.”
聪明的你也明白了吗?
(1)归纳(加乘)运算的运算法则:
两数进行(加乘)运算时,运算法则是什么.
特别地,0和任何数进行(加乘)运算,或任何数和0进行(加乘)运算运算法则是什么.
(2)计算:
①(![]() )[
)[![]() (
(![]() )].(括号的作用与它在有理数运算中的作用一致)
)].(括号的作用与它在有理数运算中的作用一致)
② 若(![]() )(
)(![]()
![]() )
)![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为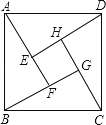
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com