
����Ŀ����ͼ,A��B��C�������ϵ�����,O��ԭ��,BO=3,AB=2BO,5AO=3CO.
(1)д�������ϵ�A��C��ʾ����;
(2)��P��Q�ֱ��A��Cͬʱ����,��P��ÿ��2����λ���ȵ��ٶ����������������˶�,��Q��ÿ��6����λ���ȵ��ٶ����������������˶�,MΪ�߶�AP���е�,��N���߶�CQ��,��CN=![]() CQ.���˶���ʱ��Ϊt(t>0)��.
CQ.���˶���ʱ��Ϊt(t>0)��.
�������ϵ�M��N��ʾ�����ֱ�����������(�ú�t��ʽ�ӱ�ʾ);
��tΪ��ֵʱ,M��N���㵽ԭ��ľ������?
![]()
���𰸡���1��-9��15����2����t-9��15-4t.��t=2��t=![]()
��������
��1������ͼʾ����֪���������A��C��ʾ�����ֱ���-9��15��
��2���ٸ������⣬ֱ��д����M��N��ʾ�����ֱ���t-9��15-4t��
�ڷ������ۣ���M��ԭ����࣬��N��ԭ���Ҳࣻ��M��N����ԭ����࣮
(1)��A��C��ʾ�����ֱ���-9��15.
(2)�ٵ�M��N��ʾ�����ֱ���t-9��15-4t.
�ڵ���M��ԭ�����,��N��ԭ���Ҳ�ʱ,�������֪9-t=15-4t.
���������,��t=2.
����M��N����ԭ�����ʱ,�������֪t-9=15-4t.
���������,��t=![]() .
.
���������֪,��M��N����ͬʱ��ԭ���Ҳ�.
���Ե�t=2��t=![]() ʱ,M��N���㵽ԭ��ľ������.
ʱ,M��N���㵽ԭ��ľ������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��AD��BC��CE��AB��AE=CE����֤��

��1����AEF�ա�CEB��
��2��AF=2CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ���ָ�����㣬�ó���һ���µ����㣬��������������Ӧ��ϵ��һ��ʵ����
ָ������ | 21=2 | 22=4 | 23=8 | �� | 31=3 | 32=9 | 33=27 | �� |
������ | log22=1 | log24=2 | log28=3 | �� | log33=1 | log39=2 | log327=3 | �� |
�����ϱ����ɣ�ijͬѧд��������ʽ�ӣ���log216=4����log525=5����log2 ![]() =��1��������ȷ���ǣ�������
=��1��������ȷ���ǣ�������
A.�٢�
B.�٢�
C.�ڢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx��3��������1��0������3��0�����㣬��y�ύ�ڵ�C��ֱ��y=kx�������߽���A��B���㣮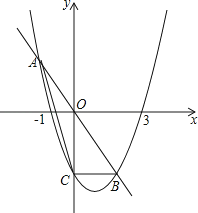
��1��д����C�����겢����������ߵĽ���ʽ��
��2����ԭ��OΪ�߶�AB���е�ʱ����k��ֵ��A��B��������ꣻ
��3���Ƿ����ʵ��kʹ�á�ABC�����Ϊ ![]() �������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� OC �ڡ�AOB ���ڲ������� OE ƽ�֡�AOC������ OF ƽ�֡�COB��
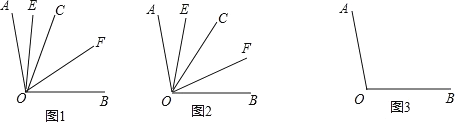
��1����ͼ 1������AOB=100������AOC=32�������EOF= �ȣ�
��2������AOB=������AOC=����
����ͼ 2�������� OC �ڡ�AOB ���ڲ��Ƶ� O ��ת�����EOF �Ķ�����
�������� OC �ڡ�AOB ���ⲿ�Ƶ� O ��ת(��ת�С�AOC����BOC ����ָС�� 180���Ľ�)�������������䣬�����ͼ 3 ̽����EOF �Ĵ�С��ֱ��д����EOF �Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У���C��90�㣬AC��BC��ADƽ�֡�CAB����BC��D���ܷ���AB��ȷ��һ��E��ʹ��BDE���ܳ�����AB�ij�?��˵�����ɣ�
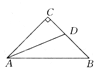
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC��Rt��OCD�У���ACB=��DCO=90�㣬OΪAB���е㣮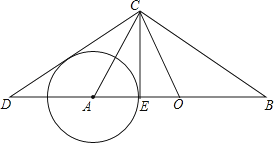
��1����֤����B=��ACD��
��2����֪��E��AB�ϣ���BC2=ABBE��
��i����tan��ACD= ![]() ��BC=10����CE�ij���
��BC=10����CE�ij���
��ii�����ж�CD����AΪԲ�ġ�AEΪ�뾶�ġ�A��λ�ù�ϵ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��������ֱ���A����2��0����B��0��1�����㣬�뷴����������ͼ���ڵ�һ�����ڵ�C��4��n������һ�κ����ͷ����������Ľ���ʽ��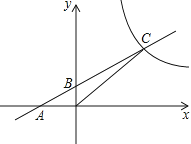
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ�����ϣ�Ϊ����֤�������ϵ���������� 10 �����г��أ�ÿ���� 50 ǧ��Ϊ�����������ּ�Ϊ�������㲿�ּ�Ϊ����10 ���������ֱ����£�+5����3����8��+6��+4��+8����2����12��+8��+5
��1����ÿ�� 50 ǧ��Ϊ��������� 10 �����ϵ����������������ǧ�ˣ�
��2���������������Ϲ��� 500 �������������ϵ�������ԼΪ���٣�
��3������ÿ�� 120 Ԫ������140 Ԫ�������������������ϵ��������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com