
ЁОЬтФПЁПвбжЊЩфЯп OC дкЁЯAOB ЕФФкВПЃЌЩфЯп OE ЦНЗжЁЯAOCЃЌЩфЯп OF ЦНЗжЁЯCOBЃЎ
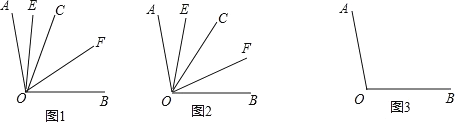
ЃЈ1ЃЉШчЭМ 1ЃЌШєЁЯAOB=100ЁуЃЌЁЯAOC=32ЁуЃЌдђЁЯEOF= ЖШЃЛ
ЃЈ2ЃЉШєЁЯAOB=ІСЃЌЁЯAOC=ІТЃЎ
ЂйШчЭМ 2ЃЌШєЩфЯп OC дкЁЯAOB ЕФФкВПШЦЕу O а§зЊЃЌЧѓЁЯEOF ЕФЖШЪ§ЃЛ
ЂкШєЩфЯп OC дкЁЯAOB ЕФЭтВПШЦЕу O а§зЊ(а§зЊжаЁЯAOCЁЂЁЯBOC ОљЪЧжИаЁгк 180ЁуЕФНЧ)ЃЌЦфгрЬѕМўВЛБфЃЌЧыНшжњЭМ 3 ЬНОПЁЯEOF ЕФДѓаЁЃЌжБНгаДГіЁЯEOF ЕФЖШЪ§ЃЎ
ЁОД№АИЁПЂХ50ЁуЃЛЂЦЂй ![]() ІСЃЛЂк
ІСЃЛЂк ![]() ІСЛђ 180Ёу-
ІСЛђ 180Ёу-![]() ІС.
ІС.
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЁЯBOCЖШЪ§ЃЌИљОнНЧЦНЗжЯпЖЈвхЧѓГіЁЯEOCКЭЁЯFOCЖШЪ§ЃЌЧѓКЭМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉЂйИљОнНЧЦНЗжЯпЖЈвхЕУГіЁЯCOE![]() ЁЯAOCЃЌЁЯCOF
ЁЯAOCЃЌЁЯCOF![]() ЁЯBOCЃЌЧѓГіЁЯEOFЃНЁЯEOC+ЁЯFOC
ЁЯBOCЃЌЧѓГіЁЯEOFЃНЁЯEOC+ЁЯFOC![]() ЁЯAOBЃЌДњШыЧѓГіМДПЩЃЛ
ЁЯAOBЃЌДњШыЧѓГіМДПЩЃЛ
ЂкЗжСНжжЧщПіЃКaЃЎЩфЯпOEЃЌOFжЛга1ИідкЁЯAOBЭтУцЃЌИљОнНЧЦНЗжЯпЖЈвхЕУГіЁЯCOE![]() ЁЯAOCЃЌЁЯCOF
ЁЯAOCЃЌЁЯCOF![]() ЁЯBOCЃЌЧѓГіЁЯEOFЃНЁЯFOCЉЁЯCOE
ЁЯBOCЃЌЧѓГіЁЯEOFЃНЁЯFOCЉЁЯCOE![]() ЁЯAOBЃЛ
ЁЯAOBЃЛ
bЃЎЩфЯпOEЃЌOF2ИіЖМдкЁЯAOBЭтУцЃЌИљОнНЧЦНЗжЯпЖЈвхЕУГіЁЯEOF![]() ЁЯAOCЃЌЁЯCOF
ЁЯAOCЃЌЁЯCOF![]() ЁЯBOCЃЌЧѓГіЁЯEOFЃНЁЯEOC+ЁЯCOF
ЁЯBOCЃЌЧѓГіЁЯEOFЃНЁЯEOC+ЁЯCOF![]() ЃЈ360ЁуЉЁЯAOBЃЉЃЌДњШыЧѓГіМДПЩЃЎ
ЃЈ360ЁуЉЁЯAOBЃЉЃЌДњШыЧѓГіМДПЩЃЎ
ЃЈ1ЃЉЁпЁЯAOBЃН100ЁуЃЌЁЯAOCЃН32ЁуЃЌЁрЁЯBOCЃНЁЯAOBЉЁЯAOCЃН68ЁуЃЎ
ЁпOEЃЌOFЗжБ№ЪЧЁЯAOCКЭЁЯCOBЕФНЧЦНЗжЯпЃЌЁрЁЯEOC![]() ЁЯAOCЃН16ЁуЃЌЁЯFOC
ЁЯAOCЃН16ЁуЃЌЁЯFOC![]() ЁЯBOCЃН34ЁуЃЌЁрЁЯEOFЃНЁЯEOC+ЁЯFOCЃН16Ёу+34ЁуЃН50ЁуЃЛ
ЁЯBOCЃН34ЁуЃЌЁрЁЯEOFЃНЁЯEOC+ЁЯFOCЃН16Ёу+34ЁуЃН50ЁуЃЛ
ЃЈ2ЃЉЂйЁпOEЃЌOFЗжБ№ЪЧЁЯAOCКЭЁЯCOBЕФНЧЦНЗжЯпЃЌЁрЁЯEOC![]() ЁЯAOCЃЌЁЯFOC
ЁЯAOCЃЌЁЯFOC![]() ЁЯBOCЃЌЁрЁЯEOFЃНЁЯEOC+ЁЯFOC
ЁЯBOCЃЌЁрЁЯEOFЃНЁЯEOC+ЁЯFOC![]() ЁЯAOB
ЁЯAOB![]() ІСЃЛ
ІСЃЛ
ЂкЗжСНжжЧщПіЬжТлЃКaЃЎЩфЯпOEЃЌOFжЛга1ИідкЁЯAOBЭтУцЃЌШчЭМ3ЂйЃЌЁЯEOFЃНЁЯFOCЉЁЯCOE![]() ЁЯBOC
ЁЯBOC![]() ЁЯAOC
ЁЯAOC![]() ЃЈЁЯBOCЉЁЯAOCЃЉ
ЃЈЁЯBOCЉЁЯAOCЃЉ![]() ЁЯAOB=
ЁЯAOB=![]() ІСЃЛ
ІСЃЛ
bЃЎЩфЯпOEЃЌOF2ИіЖМдкЁЯAOBЭтУцЃЌШчЭМ3ЂкЃЌЁЯEOFЃНЁЯEOC+ЁЯCOF![]() ЁЯAOC
ЁЯAOC![]() ЁЯBOC
ЁЯBOC![]() ЃЈЁЯAOC+ЁЯBOCЃЉ
ЃЈЁЯAOC+ЁЯBOCЃЉ![]() ЃЈ360ЁуЉЁЯAOBЃЉ180ЁуЃ
ЃЈ360ЁуЉЁЯAOBЃЉ180ЁуЃ![]() ЁЯAOB=180ЁуЃ
ЁЯAOB=180ЁуЃ![]() ІСЃЎ
ІСЃЎ
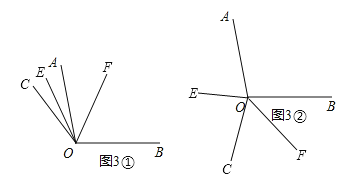
ЙЪЁЯEOFЕФЖШЪ§ЪЧ![]() ІСЛђ180ЁуЃ
ІСЛђ180ЁуЃ![]() ІСЃЎ
ІСЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋСЌајЕФЦцЪ§1ЁЂ3ЁЂ5ЁЂ7 ЁЁ ЃЌХХСаГЩШчЯТЕФЪ§БэЃЌгУЪЎзжПђПђГі5ИіЪ§ЁЃ
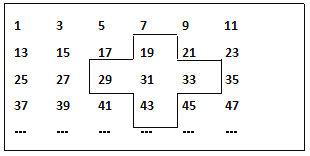
ЮЪЃК(1)ЪЎзжПђПђГі5ИіЪ§зжЕФКЭгыПђзге§жаМфЕФЪ§31гаЪВУДЙиЯЕЃП
(2)ШєНЋЪЎзжПђЩЯЯТзѓгвЦНвЦЃЌПЩПђзЁСэЭт5ИіЪ§ЃЌШєЩшжаМфЕФЪ§ЮЊaЃЌгУДњЪ§ЪНБэЪОЪЎзжПђПђзЁЕФ5ИіЪ§зжжЎКЭЃЛ
(3)ЪЎзжПђПђзЁЕФ5ИіЪ§зжжЎКЭФмЕШгк2000Т№ЃПШєФмЃЌЗжБ№аДГіЪЎзжПђПђзЁЕФ5ИіЪ§ЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЯТЙмЕРЃЌШєгЩМзЖгЕЅЖРЦЬЩшЃЌЧЁКУдкЙцЖЈЪБМфФкЭъГЩЃЛШєгЩввЖгЕЅЖРЦЬЩшЃЌашвЊГЌЙ§ЙцЖЈЪБМф15ЬьВХФмЭъГЩЃЌШчЙћЯШгЩМзЁЂввСНЖгКЯзі10ЬьЃЌдйгЩввЖгЕЅЖРЦЬЩше§КУАДЪБЭъГЩЃЎ
ЃЈ1ЃЉетЯюЙЄГЬЕФЙцЖЈЪБМфЪЧЖрЩйЬьЃП
ЃЈ2ЃЉвбжЊМзЖгУПЬьЕФЪЉЙЄЗбгУЮЊ5000дЊЃЌввЖгУПЬьЕФЪЉЙЄЗбгУЮЊ3000дЊЃЌЮЊСЫЫѕЖЬЙЄЦквдМѕЩйЖдОгУёНЛЭЈЕФгАЯьЃЌЙЄГЬжИЛгВПзюжеОіЖЈИУЙЄГЬгЩМзЁЂввСНЖгКЯзіРДЭъГЩЃЌФЧУДИУЙЄГЬЪЉЙЄЗбгУЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
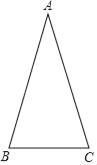
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌЕуDдкABБпЩЯЃЌЕуDЕНЕуAЕФОрРыгыЕуDЕНЕуCЕФОрРыЯрЕШЃЎ
ЃЈ1ЃЉРћгУГпЙцзїЭМзїГіЕуDЃЌВЛаДзїЗЈЕЋБЃСєзїЭМКлМЃЃЎ
ЃЈ2ЃЉШєЁїABCЕФЕзБпГЄ5ЃЌжмГЄЮЊ21ЃЌЧѓЁїBCDЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬНОПЃК
ЂйаТжЊбЇЯА
ШєАбНЋвЛИіЦНУцЭМаЮЗжЮЊУцЛ§ЯрЕШЕФСНИіВПЗжЕФжБЯпНазіИУЦНУцЭМаЮЕФЁАУцЯпЁБЃЌЦфЁАУцЯпЁББЛИУЦНУцЭМаЮНиЕУЕФЯпЖЮНазіИУЦНУцЭМаЮЕФЁАУцОЖЁБЃЈР§ШчдВЕФжБОЖОЭЪЧдВЕФЁАУцОЖЁБЃЉЃЎ
ЂкНтОіЮЪЬт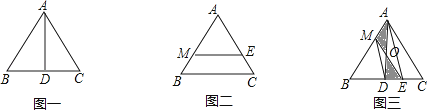
вбжЊЕШБпШ§НЧаЮABCЕФБпГЄЮЊ2ЃЎ
ЃЈ1ЃЉШчЭМвЛЃЌШєADЁЭBCЃЌДЙзуЮЊDЃЌЪдЫЕУїADЪЧЁїABCЕФвЛЬѕУцОЖЃЌВЂЧѓADЕФГЄЃЛ
ЃЈ2ЃЉШчЭМЖўЃЌШєMEЁЮBCЃЌЧвMEЪЧЁїABCЕФвЛЬѕУцОЖЃЌЧѓУцОЖMEЕФГЄЃЛ
ЃЈ3ЃЉШчЭМШ§ЃЌвбжЊDЮЊBCЕФжаЕуЃЌСЌНгADЃЌMЮЊABЩЯЕФвЛЕуЃЈ0ЃМAMЃМ1ЃЉЃЌEЪЧDCЩЯЕФвЛЕуЃЌСЌНгMEЃЌMEгыADНЛгкЕуOЃЌЧвSЁїMOA=SЁїDOE ЃЎ
ЂйЧѓжЄЃКMEЪЧЁїABCЕФУцОЖЃЛ
ЂкСЌНгAEЃЌЧѓжЄЃКMDЁЮAEЃЛ
ЃЈ4ЃЉЧыФуВТВтЕШБпШ§НЧаЮABCЕФУцОЖГЄlЕФШЁжЕЗЖЮЇЃЈжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,AЁЂBЁЂCЪЧЪ§жсЩЯЕФШ§Еу,OЪЧдЕу,BO=3,AB=2BO,5AO=3CO.
(1)аДГіЪ§жсЩЯЕуAЁЂCБэЪОЕФЪ§;
(2)ЕуPЁЂQЗжБ№ДгAЁЂCЭЌЪБГіЗЂ,ЕуPвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђгвдШЫйдЫЖЏ,ЕуQвдУПУы6ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏ,MЮЊЯпЖЮAPЕФжаЕу,ЕуNдкЯпЖЮCQЩЯ,ЧвCN=![]() CQ.ЩшдЫЖЏЕФЪБМфЮЊt(t>0)Уы.
CQ.ЩшдЫЖЏЕФЪБМфЮЊt(t>0)Уы.
ЂйЪ§жсЩЯЕуMЁЂNБэЪОЕФЪ§ЗжБ№ЪЧЁЁЁЁЁЁЁЁ(гУКЌtЕФЪНзгБэЪО);
ЂкtЮЊКЮжЕЪБ,MЁЂNСНЕуЕНдЕуЕФОрРыЯрЕШ?
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГізтГЕМнЪЛдБДгЙЋЫОГіЗЂЃЌдкФЯББЯђЕФШЫУёТЗЩЯСЌајНгЫЭ5ХњПЭШЫЃЌааЪЛТЗГЬМЧТМШчЯТЃЈЙцЖЈЯђФЯЮЊе§ЃЌЯђББЮЊИКЃЌЕЅЮЛЃКkmЃЉЃК

ЂйНгЫЭЭъЕк5ХњПЭШЫКѓЃЌИУМнЪЛдБдкЙЋЫОЪВУДЗНЯђЃЌОрРыЙЋЫОЖрЩйЧЇУзЃП
ЂкШєИУГізтГЕУПЧЇУзКФгЭ0.2Щ§ЃЌФЧУДдкетЙ§ГЬжаЙВКФгЭЖрЩйЩ§ЃП
ЂлШєИУГізтГЕЕФМЦМлБъзМЮЊЃКааЪЛТЗГЬВЛГЌЙ§3kmЪеЗб10дЊЃЌГЌЙ§3kmЕФВПЗжАДУПЧЇУзМг1.8дЊЪеЗбЃЌдкетЙ§ГЬжаИУМнЪЛдБЙВЪеЕНГЕЗбЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦјЯѓЬЈЗЂЯжЃКдкФГЖЮЪБМфРяЃЌШчЙћдчГПЯТгъЃЌФЧУДЭэЩЯЪЧЧчЬьЃЛШчЙћЭэЩЯЯТгъЃЌФЧУДдчГПЪЧЧчЬьЃЌвбжЊетЖЮЪБМфга9ЬьЯТСЫгъЃЌВЂЧвга6ЬьЭэЩЯЪЧЧчЬьЃЌ7ЬьдчГПЪЧЧчЬьЃЌдђетвЛЖЮЪБМфгаЃЈЁЁЁЁЃЉ
A.9Ьь
B.11Ьь
C.13Ьь
D.22Ьь
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїдкбЇЯАСЫЁЖеЙПЊгыелЕўЁЗетвЛПЮКѓЃЌУїАзСЫКмЖрМИКЮЬхЖМФмеЙПЊГЩЦНУцЭМаЮЃЎгкЪЧЫћдкМвгУМєЕЖеЙПЊСЫвЛИіГЄЗНЬхжНКаЃЌПЩЪЧвЛВЛаЁаФЖрМєСЫвЛЬѕРтЃЌАбжНКаМєГЩСЫСНВПЗжЃЌМДЭМжаЕФЂйКЭЂкЃЎИљОнФуЫљбЇЕФжЊЪЖЃЌЛиД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉаЁУїзмЙВМєПЊСЫ_______ЬѕРтЃЎ
ЃЈ2ЃЉЯждкаЁУїЯыНЋМєЖЯЕФЂкжиаТеГЬљЕНЂйЩЯШЅЃЌЖјЧвОЙ§елЕўвдКѓЃЌШдШЛПЩвдЛЙдГЩвЛИіГЄЗНЬхжНКаЃЌФуШЯЮЊЫћгІИУНЋМєЖЯЕФжНЬѕеГЬљЕНЂйжаЕФЪВУДЮЛжУЃПЧыФуАяжњаЁУїдкЂйЩЯВЙШЋЃЎ
ЃЈ3ЃЉаЁУїЫЕЃКЫћЫљМєЕФЫљгаРтжаЃЌзюГЄЕФвЛЬѕРтЪЧзюЖЬЕФвЛЬѕРтЕФ5БЖЃЎЯждквбжЊетИіГЄЗНЬхжНКаЕФЕзУцЪЧвЛИіе§ЗНаЮЃЌВЂЧветИіГЄЗНЬхжНКаЫљгаРтГЄЕФКЭЪЧ880cmЃЌЧѓетИіГЄЗНЬхжНКаЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com