
【题目】某地下管道,若由甲队单独铺设,恰好在规定时间内完成;若由乙队单独铺设,需要超过规定时间15天才能完成,如果先由甲、乙两队合做10天,再由乙队单独铺设正好按时完成.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为5000元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民交通的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,那么该工程施工费用是多少?
【答案】(1)这项工程的规定时间是30天;(2)该工程的费用为144000元.
【解析】
(1)设这项工程的规定时间是x天,根据题意得:(![]() +
+![]() )×10+
)×10+![]() =1.解方程可得;(2)该工程由甲、乙队合做完成,所需时间为:1÷(
=1.解方程可得;(2)该工程由甲、乙队合做完成,所需时间为:1÷(![]() +
+![]() )=18(天),则该工程施工费用是:18×(5000+3000)元.
)=18(天),则该工程施工费用是:18×(5000+3000)元.
(1)设这项工程的规定时间是x天,根据题意得:
(![]() +
+![]() )×10+
)×10+![]() =1.
=1.
解得:x=30.
经检验x=30是原分式方程的解.
答:这项工程的规定时间是30天.
(2)该工程由甲、乙队合做完成,所需时间为:1÷(![]() +
+![]() )=18(天),
)=18(天),
则该工程施工费用是:18×(5000+3000)=144000(元),
答:该工程的费用为144000元.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
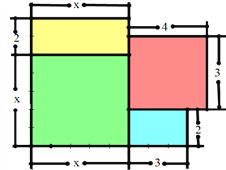
【题目】李叔叔在“中央山水”买了一套经济适用房,他准备将地面铺上地砖,这套住宅的建筑平面(由四个长方形组成)如图所示(图中长度单位:米),请解答下问题:
(1)用式子表示这所住宅的总面积;
(2)若铺1平方米地砖平均费用120元,求当x=6时,这套住宅铺地砖总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;……;则第10个图形中,其中看得见的小立方体个数是( )
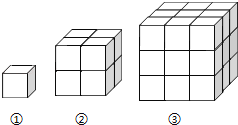
A. 270 B. 271 C. 272 D. 273
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足(b﹣3)2+|c+4|=0,且a,b,c分别是点A,B,C在数轴上对应的数.
![]()
(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2 ![]() =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线 OC 在∠AOB 的内部,射线 OE 平分∠AOC,射线 OF 平分∠COB.
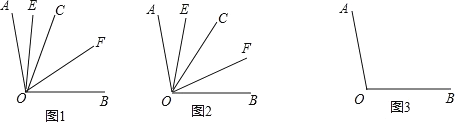
(1)如图 1,若∠AOB=100°,∠AOC=32°,则∠EOF= 度;
(2)若∠AOB=α,∠AOC=β.
①如图 2,若射线 OC 在∠AOB 的内部绕点 O 旋转,求∠EOF 的度数;
②若射线 OC 在∠AOB 的外部绕点 O 旋转(旋转中∠AOC、∠BOC 均是指小于 180°的角),其余条件不变,请借助图 3 探究∠EOF 的大小,直接写出∠EOF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线![]() :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com