
【题目】如图1,在![]() 中,点D、E分别在AB、AC上,
中,点D、E分别在AB、AC上,![]() ,
,![]() ,
,
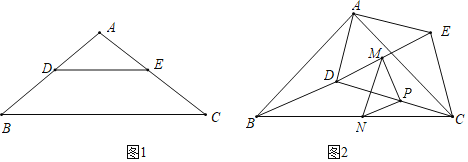
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
,把![]() 绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 把
把![]() 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若![]() ,
,![]() ,试问
,试问![]() 面积是否存在最大值;若存在,求出其最大值
面积是否存在最大值;若存在,求出其最大值![]() 若不存在,请说明理由.
若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,弦AB、CD相交点P,弦CA、BD的延长线交于S,∠APD=2m°,∠PAC=m°+15°.
(1)求∠S的度数;
(2)连AD,BC,若![]() ,求m的值.
,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知:点A(2016,0)、B(0,2018),以AB为斜边在直线AB下方作等腰直角△ABC,则点C的坐标为( )
A. (2,2 )B. (2,﹣2 )C. (﹣1,1 )D. (﹣1,﹣1 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
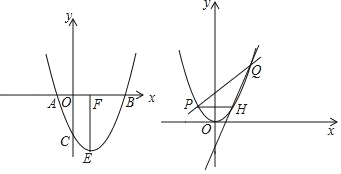
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列命题完成以下问题。(命题)若![]() 、
、![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根,则有
的两个实数根,则有![]() ,
,![]() 。
。
〖问题1〗若![]() 、
、![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根,则有
的两个实数根,则有![]() ____________,
____________,![]() ___________。
___________。
〖问题2〗若![]() 、
、![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,则有
的两个实数根,则有![]() ____________,
____________,![]() ___________。
___________。
〖问题3〗甲、乙两同学解同一道一元二次方程![]() 时,甲看错了一次项系数,得两根为2和7,乙看错了常数项,得两根为1和-10。根据这些数据,你能否确定原来正确的方程?如果能,请写出原方程,并写出你的推导过程;如果不能,请说明理由。
时,甲看错了一次项系数,得两根为2和7,乙看错了常数项,得两根为1和-10。根据这些数据,你能否确定原来正确的方程?如果能,请写出原方程,并写出你的推导过程;如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
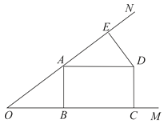
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
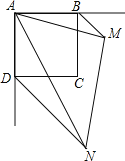
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
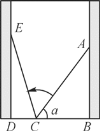
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com