
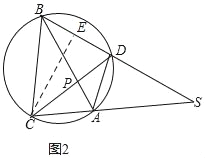
【题目】如图,⊙O中,弦AB、CD相交点P,弦CA、BD的延长线交于S,∠APD=2m°,∠PAC=m°+15°.
(1)求∠S的度数;
(2)连AD,BC,若![]() ,求m的值.
,求m的值.

【答案】(1) 30°;(2) m=45
【解析】
(1)由圆周角定理可知:∠PAC=∠PDB=m°+15°,从而可知∠PDS=∠PAS,由于∠APD=2m°,利用四边形内角和即可得出∠S的度数;
(2)过点C作CE⊥BD于点E,由圆内接四边形的性质可知:∠DAS=∠SBC,从而可证明△SAD∽△SBC,从而可求出ED、CE的长度,从而可得出∠ECD的度数,进而求出m的值.
(1)由圆周角定理可知:∠PAC=∠PDB=m°+15°,
∴∠PDS=∠PAS=180﹣(m°+15°)=165°﹣m°,
∵∠APD=2m°,
∴∠S=360°﹣∠PDS﹣∠PAS﹣∠APD
=360°﹣2(165°﹣m°)﹣2m°
=30°,
(2)过点C作CE⊥BD于点E,
由圆内接四边形的性质可知:∠DAS=∠SBC,
∵∠S=∠S,
∴△SAD∽△SBC,
∴![]() ,
,
设SD=1,SC=![]() ,
,
∵∠S=30°,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴∠ECD=30°,
∴∠EDC=60°,
∴m°+15°=60°,
∴m=45.


科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
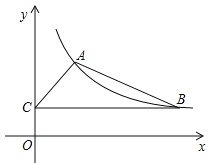
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 函数图象分别位于第一、第三象限
B. 当x>0时,y随x的增大而减小
C. 函数图象经过点(1,2)
D. 若点A(x1,y1),B(x2,y2)都在函数图象上,且x1<x2,则y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某五金商店准备从机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用900元正好可以购进50个甲种零件和50个乙种零件.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出该五金商店本次从机械厂购进甲、乙两种零件有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
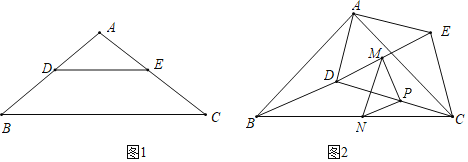
【题目】如图1,在![]() 中,点D、E分别在AB、AC上,
中,点D、E分别在AB、AC上,![]() ,
,![]() ,
,
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
,把![]() 绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 把
把![]() 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若![]() ,
,![]() ,试问
,试问![]() 面积是否存在最大值;若存在,求出其最大值
面积是否存在最大值;若存在,求出其最大值![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com