

分析 (1)把k=0.1,t=0.5,v=10代入即可得到刹车距离;
(2)把k=0.1,v=15,s=52.5代入所给关系式可得t的值;
(3)把k=0.1,v=8,t=2与0.5分别代入所给关系式可得刹车距离,再相减即可;
(4)把k=0.1,v=15,s=45代入所给关系式,求得t的值即可.
解答 解:(1)当k=0.1,t=0.5,v=10时,
s=0.5×10+0.1×102=15m.
故答案为:15;
(2)52.5=15t+0.1×152,
解得t=2.
故答案为2;
(3)当t=2,v=8时,s=2×8+0.1×82=22.4(米),
当t=0.5,v=8时,s=0.5×8+0.1×82=10.4(米),
22.4-10.4=12(米).
答:刹车距离将比未饮酒时增加12米;
(4)当v=15,s=45时,
45=15t+0.1×152,
解得t=1.5.
所以,反应时间应不超过1.5秒.
点评 主要考查一元一次方程的应用;选择合适的数值代入所给关系式求解是解决本题的易错点.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
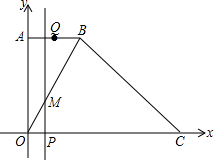 如图,在平面直角坐标系中,已知A(0,4),B(2,4),点C在x轴的正半轴上,且∠BCO=45°,连接OB.动点Q以每秒1个单位长度的速度,从点B沿折线B-A-O向点O运动.同时动点P以相同的速度,从点O沿线段OC向点C运动.过点P作直线PM⊥OC,与折线O-B-C相交于点M.当其中一点到达终点时,另一点也随之停止运动.设点P运动时间为t(秒).
如图,在平面直角坐标系中,已知A(0,4),B(2,4),点C在x轴的正半轴上,且∠BCO=45°,连接OB.动点Q以每秒1个单位长度的速度,从点B沿折线B-A-O向点O运动.同时动点P以相同的速度,从点O沿线段OC向点C运动.过点P作直线PM⊥OC,与折线O-B-C相交于点M.当其中一点到达终点时,另一点也随之停止运动.设点P运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
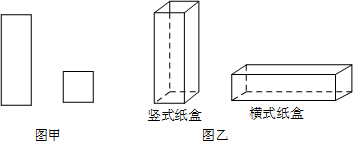
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | 100-x | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com