
��ɽֲ��������A��B����������֪A��Ϊ�����Σ���Ϊ��x+y���ף���Ϊ��x��y���ף�B��Ϊ�����Σ��߳�Ϊ��x+3y���ף�
��1�����ô���ʽ��ʾA��B���������֮�Ͳ�����
��2���ָ���ʵ����Ҫ��A���������ģ������ӣ�11x��y���ף������٣�x��2y���ף����ĺ�A���ij��ȿ���350�ף������ĺ��������ܳ�֮��Ϊ980�ף�
����x��y��ֵ��
����A��ȫ����ֲC�ֻ���B��ȫ����ֲD�ֻ�����C��D���ֻ�Ͷ��ķ����������ο͵����������
|
| C | D |
| Ͷ�루Ԫ/ƽ���ף� | 12 | 16 |
| ���棨Ԫ/ƽ���ף� | 18 | 26 |
�����ĺ�A��B�������εľ�����֮�ͣ���������=���橁Ͷ�룩
�����㡿��ʽ�Ļ�����㣮
��ר�⡿Ӧ���⣮
����������1�����ݳ����ε������ʽ�������ε������ʽ�ֱ����A��B���������������Ӽ�����⣻
��2���ٸ��ݵ�����ϵ�����ĺ�A���ij��ȿ���350�ף����ĺ��������ܳ�֮��Ϊ980�ף��г����������x��y��ֵ��
�ڴ�����ֵ�õ����ĺ�A��B���������֮�ͣ��ٸ��ݾ�����=���橁Ͷ�룬��ʽ���㼴����⣮
����𡿽⣺��1����x+y����x��y��+��x+3y����x+3y��
=x2��y2+x2+6xy+9y2
=2x2+6xy+8y2��ƽ���ף�
��A��B���������֮��Ϊ��2x2+6xy��ƽ���ף�
��2����x+y��+��11x��y��
=x+y+11x��y
=12x���ף���
��x��y������x��2y��
=x��y��x+2y
=y���ף���
��������

 ��
��
���
 ��
��
12xy=12��30��10=3600��ƽ���ף���
��x+3y����x+3y��
=x2+6xy+9y2
=900+1800+900
=3600��ƽ���ף���
��18��12����3600+��26��16����3600
=6��3600+10��3600
=57600��Ԫ����
�����ĺ�A��B�������εľ�����֮��Ϊ57600Ԫ��
�����������⿼����ʽ�Ļ�����㣬�ҳ������е���֪������δ֪��������֮��Ĺ�ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ƽ��ֱ������ϵ�У���A����2��a����B��b��3������AB=3����AB��x�ᣬ��a=��������������b=��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�����꼶�²���ѧ�̲ĸ���������ֱ�ߺ����ǰ廭ƽ���ߵķ���������
��������ֱ������ֱ֪��ƽ�е���(����)
A.��ABC =��A��B��C�� B.��BCA=��B��C��A��
C.��CAB=��C��A��B�� D.��CAA��=��C��A��A

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ�������ϱ�ʾ3��
 �Ķ�Ӧ��ֱ�ΪC��B����C��AB���е㣬���A��ʾ������ ��������
�Ķ�Ӧ��ֱ�ΪC��B����C��AB���е㣬���A��ʾ������ ��������


A��
 B��
B��
 C��
C��
 D��
D��

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�������3.14159��
 ��0.131131113������������3֮��1�ĸ�����μ�1���������У�
��0.131131113������������3֮��1�ĸ�����μ�1���������У�
 ��
��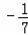
 ���������ĸ����У�������
���������ĸ����У�������
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�ֲ������������壬���İ뾶Ϊ0.00000000375���ÿ�ѧ��������ʾΪ��������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com