
| A. | m≥3 | B. | m>3 | C. | m≤-1 | D. | m<-1 |
分析 根据a=-1可得知抛物线的开口朝下,由“当x<1时,y随x的增大而增大”可得出抛物线的对称轴x≥1,结合给定二次函数解析式利用抛物线的对称轴为x=-$\frac{b}{2a}$,可得出关于m的一元一次不等式,解不等式即可得出结论.
解答 解:∵a=-1<0,
∴抛物线的开口向下,
又∵当x<1时,y随x的增大而增大,
∴抛物线的对称轴x≥1.
∵二次函数的解析式为y=-x2+(m-1)x+1,
∴抛物线的对称轴为x=-$\frac{m-1}{2×(-1)}$=$\frac{m-1}{2}$≥1,
解得:m≥3.
故选A.
点评 本题考查了二次函数的性质以及解一元一次不等式,解题的关键是根据单调性结合二次函数的性质得出关于m的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据给定的单调区间确定对称轴的范围是关键.


科目:初中数学 来源: 题型:解答题
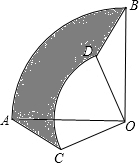 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
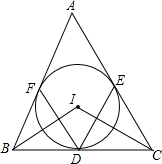 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{m}^{2}+2}$ | B. | $\sqrt{m+2}$ | C. | m2+2 | D. | m+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com