Question

【题目】探究：如图①，在矩形ABCD中，AB=3，AD=4，点P是对角线AC上的一点，过点P分别作AB、AD的平行线，交BC、CD于点M、N，求的值；

应用：如图②，在矩形ABCD中，AB=3，AD=4，点P是对角线AC上的一点，Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N，则= ．

Answer 1

【答案】；

【解析】

试题分析：探究：首先证明PN=MC，由PM∥AB，推出，即，由此即可解决问题．

应用：先过P作PG⊥BC于G，作PH⊥CD于H，判定△PGM∽△PHN，再根据相似三角形的性质以及探究的结论即可解决问题；

试题解析：探究：解：如图①中，

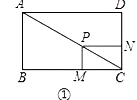
∵四边形ABCD是矩形，

∴∠B=∠DCB=90°，AD=BC=4

∵PM⊥BC，PN⊥CD，

∴∠PMC=∠PNC=90°，

∴四边形PMCN是矩形，

∴PC=CM，

∵∠PMC=∠B=90°，

∴PM∥AB，

∴△CPM∽△CAB，

∴，即，

∵AB=3，BC=4

∴=

应用：解：如图②中，过P作PG⊥BC于G，作PH⊥CD于H，则∠PGM=∠PHN=90°，∠GPH=90°，

∵Rt△PEF中，∠FPE=90°

∴∠GPM=∠HPN

∴△PGM∽△PHN

∴，

由条件可知，=，

∴=．