
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am-b).
其中所有正确的结论是( )

A. ①②③ B. ①③④ C. ①②③⑤ D. ①③⑤
【答案】D
【解析】试题分析:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+4c=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(﹣![]() ,0),
,0),
当x=﹣![]() 时,y=0,即a(﹣
时,y=0,即a(﹣![]() )2+b×(﹣
)2+b×(﹣![]() )+c=0,
)+c=0,
整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,
∴a﹣b+c>m2a﹣mb+c(m≠1),
∴a﹣b>m(am﹣b),所以⑤正确;
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】任意抛掷一枚骰子两次,骰子停止转动后,计算朝上的点数的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①点数的和为7;②点数的和为1;③点数的和为15.哪些是不可能性事件?哪些是不确定事件?
(3)点数的和为7与点数的和为2的可能性谁大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,过点P分别作AB、AD的平行线,交BC、CD于点M、N,求![]() 的值;
的值;
应用:如图②,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N,则![]() = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.
如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第1次“移位”,这时他到达编号为1的点,那么他应走1段弧长,即从1→2为第2次“移位”.
若小明从编号为4的点开始,第1次“移位”后,他到达编号为 的点,…,第2016次“移位”后,他到达编号为 的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是弹力墙MN上一点,魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转,当转到ON位置时,则从ON位置弹回,继续向OM位置旋转;当转到OM位置时,再从OM的位置弹回,继续转向ON位置,…,如此反复.按照这种方式将魔法棒进行如下步骤的旋转:第1步,从OA0(OA0在OM上)开始旋转α至OA1;第2步,从OA1开始继续旋转2α至OA2;第3步,从OA2开始继续旋转3α至OA3 , ….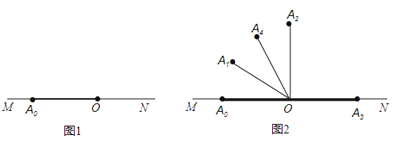
例如:当α=30°时,OA1 , OA2 , OA3 , OA4的位置如图2所示,其中OA3恰好落在ON上,∠A3OA4=120°;
当α=20°时,OA1 , OA2 , OA3 , OA4 , OA3的位置如图3所示,
其中第4步旋转到ON后弹回,即∠A3ON+∠NOA4=80°,而OA3恰好与OA2重合.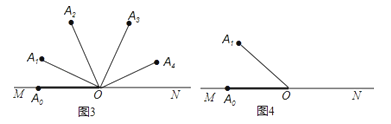
![]()
(1)若α=35°,在图4中借助量角器画出OA2 , OA3 , 其中∠A3OA2的度数是 ;
(2)若α<30°,且OA4所在的射线平分∠A2OA3 , 在如图5中画出OA1 , OA2 , OA3 , OA4并求出α的值
(3)若α<36°,且∠A2OA4=20°,则对应的α值是
(4)当OAi所在的射线是∠AiOAk(i,j,k是正整数,且OAj与OAk不重合)的平分线时,旋转停止,请探究:试问对于任意角α(α的度数为正整数,且α=180°),旋转是否可以停止?写出你的探究思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com