
【题目】如图,直线AB与CD相较于点O,OE⊥AB与点O,OB平分∠DOF,∠DOE=62°.
求∠AOC、∠EOF、∠COF的度数。

【答案】∠AOC =28°,∠EOF=118°,∠COF=124°
【解析】
根据OE⊥AB,得出∠BOE=90°,再由∠DOE=62°,得出∠BOD,由对顶角相等得出∠AOC的度数,根据角平分线的定义求出∠DOF,由∠DOF+∠DOE得出∠EOF的度数,最后由∠DOC是平角得出∠COF的度数即可.
∵OE⊥AB,
∴∠BOE=90°,
∵∠DOE=62°,
∴∠BOD=90°-62°=28°,
∴∠AOC=∠BOD=28°,
∵OB平分∠DOF,
∴∠DOF=2∠BOD=2×28°=56°,
∴∠EOF=∠DOF+∠DOE=118°
又∵点O在CD上,
∴∠COF=180°-∠DOF=180°-56°=124°.
即:∠AOC =28°,∠EOF=118°,∠COF=124°


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )

A. 40°B. 45°C. 50°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.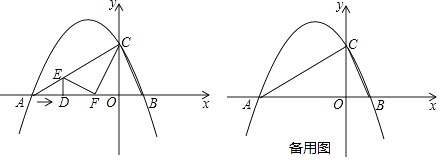
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”
(1)请写出它的逆命题 ;该逆命题是一个 命题(填“真”或“假”)
(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB、BC、AC三边的长分别是![]() ,
,![]() ,
,![]() .
.
(1)△ABC的面积是 ;
(2)请在图1中作出△ABC关于直线l对称的△A1B1C1;
(3)请在图2中画出△DEF,是DE、EF、DF三边的长分别是![]() ,
,![]() ,
,![]() ,并判断△DEF的形状,说明理由.
,并判断△DEF的形状,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
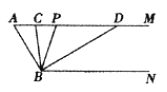
【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com