练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在菱形ABCD中，∠A=60°，AB=2，E，F两点分别从A，B两点同时出发，以相同的速度分别向终点B，C移动，连接EF，在移动的过程中，EF的最小值为（　　）

    A. 1 B. C. D.

    【答案】D

    【解析】

    连接DB，作DH⊥AB于H，如图，∵四边形ABCD为菱形，∴AD=AB=BC=CD，而∠A=60°，∴△ABD和△BCD都是等边三角形，∴∠ADB=∠DBC=60°，AD=BD，在Rt△ABH中，AH=1，AD=2，∴DH=，在△ADE和△BDF中，，∴△ADE≌△BDF，∴∠2=∠1，DE=DF，∴∠1+∠BDE=∠2+∠BDE=∠ADB=60°，∴△DEF为等边三角形，∴EF=DE，而当E点运动到H点时，DE的值最小，其最小值为，∴EF的最小值为．故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某高速铁路工程指挥部，要对某路段工程进行招标，接到了甲、乙两个工程队的投标书．从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的：若由甲队先做20天，剩下的工程再由甲、乙两队合作60天完成．

    (1)求甲、乙两队单独完成这项工程各需多少天？

    (2)已知甲队每天的施工费用为8.6万元，乙队每天的施工费用为5.4万元，工程预算的施工费用为1000万元．若在甲、乙工程队工作效率不变的情况下使施工时间最短，问拟安排预算的施工费用是否够用？若不够用，需追加预算多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣2（k﹣1）x+k2=0有两个实数根x1 ， x2 ．
    （1）求k的取值范围；
    （2）若|x1+x2|=x1x2﹣1，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 ， x2 ．
    （1）求m的取值范围；
    （2）当x12+x22=6x1x2时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障，在C处等待救援．有一救援艇位于港口A正东方向20（﹣1）海里的B处，接到求救信号后，立即沿北偏东45°方向以30海里/小时的速度前往C处救援．则救援艇到达C处所用的时间为（　　）

    A. 小时 B. 小时 C. 小时 D. 小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

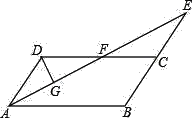
    【题目】如图，在平行四边形ABCD中，∠BAD的平分线与BC的延长线交于点E，与DC交于点F．

    （1）求证：CD=BE；

    （2）若AB=4，点F为DC的中点，DG⊥AE，垂足为G，且DG=1，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电器商场销售甲、乙两种品牌空调，已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%，用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2 台．
    （1）求甲、乙两种品牌空调的进货价；
    （2）该商场拟用不超过16000 元购进甲、乙两种品牌空调共10台进行销售，其中甲种品牌空调的售价为2500元/台，乙种品牌空调的售价为3500元/台．请你帮该商场设计一种进货方案，使得在售完这10 台空调后获利最大，并求出最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，D为△ABC内一点，∠CAD＝∠CBD＝15°，E为AD延长线上的一点，且CE＝AC.

    (1)求∠CDE的度数；

    (2)若点M在DE上，且DC＝DM，求证：ME＝BD.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两名同学相距20m，他们同时出发，同向而行，甲在乙后，图中L1、L2分别表示他们二人的路程与时间的关系，看图回答下列问题：

    （1）20s时甲跑了多少米？乙跑了多少米？

    （2）甲用几秒钟可追上乙？

    查看答案和解析>>

    同步练习册答案