Question

【题目】如图1，对称轴为直线x= 的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A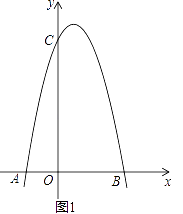

（1）求抛物线的解析式；
（2）若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；
（3）如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由对称性得：A（﹣1，0），

设抛物线的解析式为：y=a（x+1）（x﹣2），

把C（0，4）代入：4=﹣2a，

a=﹣2，

∴y=﹣2（x+1）（x﹣2），

∴抛物线的解析式为：y=﹣2x2+2x+4；

（2）

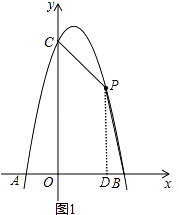
解：如图1，设点P（m，﹣2m2+2m+4），过P作PD⊥x轴，垂足为D，

∴S=S梯形+S△PDB= m（﹣2m2+2m+4+4）+ （﹣2m2+2m+4）（2﹣m），

S=﹣2m2+4m+4=﹣2（m﹣1）2+6，

∵﹣2＜0，

∴S有最大值，则S大=6；

（3）

解：存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形，

理由是：

分以下两种情况：

①当∠BQM=90°时，如图：

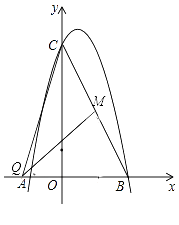
∵∠CMQ＞90°，

∴只能CM=MQ．

设直线BC的解析式为：y=kx+b（k≠0），

把B（2，0）、C（0，4）代入得： ，

解得： ，

∴直线BC的解析式为：y=﹣2x+4，

设M（m，﹣2m+4），

则MQ=﹣2m+4，OQ=m，BQ=2﹣m，

在Rt△OBC中，BC= = =2 ，

∵MQ∥OC，

∴△BMQ∽BCO，

∴ ，即 ，

∴BM= （2﹣m）=2 ﹣ m，

∴CM=BC﹣BM=2 ﹣（2 ﹣ m）= m，

∵CM=MQ，

∴﹣2m+4= m，m= =4 ﹣8．

∴Q（4 ﹣8，0）．

②当∠QMB=90°时，如图3，

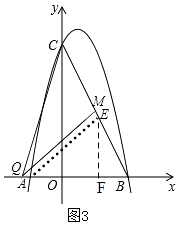
同理可设M（m，﹣2m+4），

过A作AE⊥BC，垂足为E，

∴∠EAB=∠OCB，

∴sin∠EAB= ，

∴ ，

∴BE= ，

过E作EF⊥x轴于F，

sin∠CBO= ，

∴ ，

∴EF= ，

由勾股定理得：BF= = ，

∴OF=2﹣ = ，

∴E（ ， ），

由A（﹣1，0）和E（ ， ）可得：

则AE的解析式为：y= x+ ，

则直线BC与直线AE的交点E（1.4，1.2），

设Q（﹣x，0）（x＞0），

∵AE∥QM，

∴△ABE∽△QBM，

∴ ①，

由勾股定理得：x2+42=2×[m2+（﹣2m+4﹣4）2]②，

由以上两式得：m1=4（舍），m2= ，

当m= 时，x= ，

∴Q（﹣ ，0）．

综上所述，Q点坐标为（4 ﹣8，0）或（﹣ ，0）．

【解析】（1）由对称轴的对称性得出点A的坐标，由待定系数法求出抛物线的解析式；（2）作辅助线把四边形COBP分成梯形和直角三角形，表示出面积S，化简后是一个关于S的二次函数，求最值即可；（3）画出符合条件的Q点，只有一种，①利用平行相似得对应高的比和对应边的比相等列比例式；②在直角△OCQ和直△CQM利用勾股定理列方程；两方程式组成方程组求解并取舍．