练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    化简：（x+1）2-（x+2）（x-2）．
    考点：完全平方公式,平方差公式
    专题：
    分析：先根据完全平方公式和平方差公式算乘法，再合并同类项即可．
    解答：解：原式=x2+2x+1-x2+4
    =2x+5．
    点评：本题考查了对完全平方公式和平方差公式的应用，注意：完全平方公式有：（a±b）2=a2±2ab+b2，平方差公式有（a+b）（a-b）=a2-b2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠C=90°，AC=4，sinB=
    2
    3
    ，则AB的长为（　　）
    A、6
    B、2
    		5
    C、
    18
    		13
    13
    D、
    12
    		13
    13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法不正确的是（　　）
    A、选举中，人们通常最关心的数据是众数
    B、要了解一批烟花的燃放时间，应采用抽样调查的方法
    C、若甲组数据的方差S
     
    2
    甲
    =0.05，乙组数据的方差S
     
    2
    乙
    =0.1，甲组数据比乙组数据稳定
    D、某抽奖活动的中奖率是60%，说明参加该活动10就有6次会中奖

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    △ABC的三边长为a=5，b=12，c=13，则这个三角形是（　　）
    A、等腰直角三角形
    B、等腰三角形
    C、直角三角形
    D、等边三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

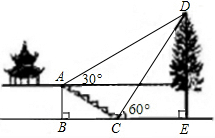    如图，兰州市某中学数学课题学习小组在“测量物体高度”的活动中，欲测量某公园内一棵古树DE的高度，他们在这棵古树的正前方一座楼亭前的台阶上A点处测得古树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得古树顶端D的仰角为60°．已知AB⊥BE于点B，且AB为4米，台阶AC的坡度为1：
    		3
    ，且B、C、E三点在同一条直线上．（根据以上条件求解下列问题时测角器的高度忽略不计）
    （1）请求出台阶AC的水平宽度BC；
    （2）如图，过点A做AF⊥DE于点F，请求出古树DE的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

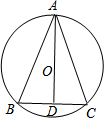    如图，已知AD既是△ABC的中线，又是角平分线，请判断：
    （1）△ABC的形状；
    （2）AD是否过△ABC外接圆的圆心O，⊙O是否是△ABC的外接圆，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

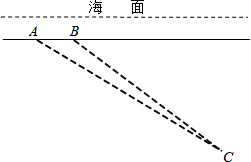    如图，一艘潜艇在海面下500米深处的A点，测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号，潜艇在同一深度保持直线航行500米，在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上，求海底黑匣子C所在点距离海面的深度．（精确到1米）（参考数据：sin36.9°≈0.60，cos36.9°≈0.80，tan36.9°≈0.75，sin31.0°≈0.51，cos31.0°≈0.87，tan31.0°≈0.60）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，甲、乙两人在一条笔直的公路上同向匀速而行，甲从A点开始追赶乙，甲、乙两人之间的距离y（m）与追赶的时间x（s）的关系如图2所示．已知乙的速度为5m/s．
    （1）求甲、乙两人之间的距离y（m）与追赶的时间x（s）之间的函数关系式；
    （2）甲从A点追赶乙，经过40s，求甲前行了多少m？
    （3）若甲追赶10s后，甲的速度增加1.2m/s，请求出10秒后甲、乙两人之间的距离y（m）与追赶的时间x （s）之间的函数关系式，并在图2中画出它的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

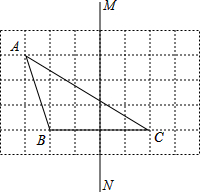    如图，在每个小正方形的边长均为l个单位长度的方格纸中，有△ABC和直线MN，点A、B、C均在小正方形的顶点上．
    （1）在图中找一点D（D点在小正方形的顶点上），使△ABC与△DBC关于直线MN对称；
    （2）连接AD、CD，请直接写出四边形ABCD的周长．

    查看答案和解析>>

    同步练习册答案