
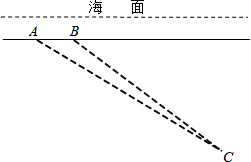
 如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31.0°≈0.51,cos31.0°≈0.87,tan31.0°≈0.60)
如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31.0°≈0.51,cos31.0°≈0.87,tan31.0°≈0.60)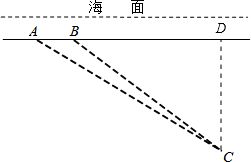 解:作CD⊥AB于D,
解:作CD⊥AB于D,| CD |
| AD |
| 5 |
| 3 |
| CD |
| BD |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为( )
如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为( )| A、24cm2 |
| B、30cm2 |
| C、48cm2 |
| D、60cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,查看答案和解析>>
科目:初中数学 来源: 题型:
| 雾霾天气对您哪方面的影响最大 | 百分比 |
| A. 身体健康 | m |
| B. 出行 | 15% |
| C.情绪不爽 | 10% |
| D. 工作学习 | n |
| E. 基本无影响 | 5% |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
| 试验总次数 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
| 1点朝上的次数 | 18 | 34 | 82 | 168 | 330 | 835 | 1660 |
| 1点朝上的频率 | 0.180 | 0.170 | 0.164 | 0.168 | 0.165 | 0.167 | 0.166 |
查看答案和解析>>
科目:初中数学 来源: 题型:
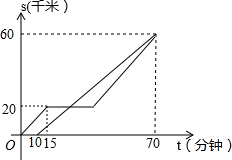 甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
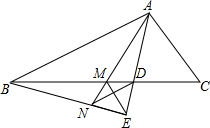 △ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.
△ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com