
分析 由直径AB的长求出半径的长,再由直径AB垂直于弦CD,利用垂径定理得到E为CD的中点,由CD的长求出CE的长,在直角三角形OCE中,利用勾股定理求出OE的长,分两种情况,即可得出AE的长.
解答 解:连接OC,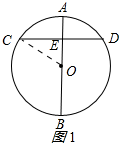
∵直径AB=10,
∴OA=OC=OB=5,
∵AB⊥CD
∴E为CD的中点,又CD=8,
∴CE=DE=4,
在Rt△OCE中,根据勾股定理得: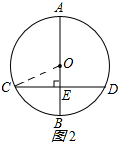 OC2=CE2+OE2,
OC2=CE2+OE2,
∴OE=3,
分两种情况:
①如图1所示:AE=OA-OE=5-3=2;
②如图2所示:AE=5+3=8;
故答案为:2或8.
点评 此题考查了垂径定理,勾股定理;熟练掌握垂径定理,由勾股定理求出OE是解本题的关键.


科目:初中数学 来源: 题型:填空题
 若将三个数-$\sqrt{3}$,$\sqrt{5}$,$\sqrt{11}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{5}$.
若将三个数-$\sqrt{3}$,$\sqrt{5}$,$\sqrt{11}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 口袋中有1个1元硬币和2个5角硬币,搅匀后从中摸出1个硬币,可能会出现的结果为1元硬币,5角硬币,5角硬币;将硬币放回再搅匀后摸出1个硬币,2次都是1元硬币的机会为$\frac{1}{9}$,都是5角硬币的机会为$\frac{2}{9}$.若用树形图表示如下,请填全.
口袋中有1个1元硬币和2个5角硬币,搅匀后从中摸出1个硬币,可能会出现的结果为1元硬币,5角硬币,5角硬币;将硬币放回再搅匀后摸出1个硬币,2次都是1元硬币的机会为$\frac{1}{9}$,都是5角硬币的机会为$\frac{2}{9}$.若用树形图表示如下,请填全.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
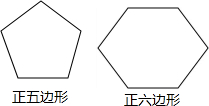 如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.
如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
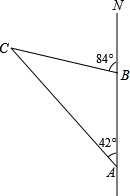 如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B处,分别从A、B处望灯塔C,测得∠MAC=42°,∠NBC=84°,则B与灯塔C的距离为180海里.
如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B处,分别从A、B处望灯塔C,测得∠MAC=42°,∠NBC=84°,则B与灯塔C的距离为180海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com