
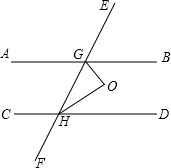
 如图:AB∥CD,GO和HO分别是∠BGH和∠GHD的角平分线.你能算出∠GOH的度数吗?如果作OP⊥AB,OQ⊥CD,OR⊥EF,你能找到图中的全等三角形吗?说明理由.
如图:AB∥CD,GO和HO分别是∠BGH和∠GHD的角平分线.你能算出∠GOH的度数吗?如果作OP⊥AB,OQ⊥CD,OR⊥EF,你能找到图中的全等三角形吗?说明理由.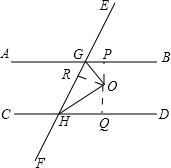


科目:初中数学 来源: 题型:
| 炮弹落点与目标距离∕m | 20 | 15 | 10 | 5 | 0 |
| 甲炮发射的炮弹个数 | 0 | 3 | 9 | 13 | 25 |
| 乙炮发射的炮弹个数 | 1 | 5 | 9 | 3 | 32 |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| a2 |
| a-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com