
【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=![]() ,∠C=45°,点P是BC边上一动点,设PB的长为x。
,∠C=45°,点P是BC边上一动点,设PB的长为x。
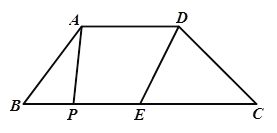
(1)梯形ABCD的面积为_________;
(2)当x的值为___________时,以点P、A、D、E为顶点的四边形为直角梯形;
(3)当x的值为___________时,以点P、A、D、E为顶点的四边形为平行四边形;
(4)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由。
【答案】(1)34
(2) x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(3)x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(4)由(3)知,①当BP=1时,不能构成菱形.
②当BP′=11时,以点P、A、D、E为顶点的四边形能构成菱形;
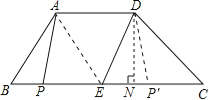
【解析】试题分析:(1)先作高,然后根据梯形的面积公式求出结果;
(2)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,容易得到AM=DN,AD=MN,而CD=![]() ,∠C=45°,由此可以求出AM=DN,又AD=5,容易求出BM、CN,若点P、A、D、E为顶点的四边形为直角梯形,则∠APC=90°或∠DPE=90°,那么P与M重合或E与N重合,即可求出此时的x的值;
,∠C=45°,由此可以求出AM=DN,又AD=5,容易求出BM、CN,若点P、A、D、E为顶点的四边形为直角梯形,则∠APC=90°或∠DPE=90°,那么P与M重合或E与N重合,即可求出此时的x的值;
(3)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,有两种情况:①当P在E的左边,利用已知条件可以求出BP的长度;②当P在E的右边,利用已知条件也可求出BP的长度;
(4)以点P、A、D、E为顶点的四边形能构成菱形.由(2)知,当BP=11时,以点P、A、D、E为顶点的四边形是平行四边形,根据已知条件分别计算一组邻边证明它们相等即可证明它是菱形.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】甲校男生占全校总人数的50%,乙校女生占全校总人数的50%,则甲乙两校女生人数相比( )
A.甲校多于乙校
B.甲校少于乙校
C.甲乙两校一样多
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
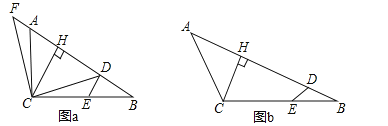
【题目】如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F.
①求证:FA=DE;
②请猜想三条线段DE,AD,CH之间的数量关系,直接写出结论;
(2)如图b,当∠ACB=120°时,三条线段DE,AD,CH之间存在怎样的数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2-(k+1)x=0有两个不相等的实数根,则k的取值范围为( )
A. k>-1 B. k<-1 C. k≠-1 D. k为任意实数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B,点A在点B的左边,点A表示的数为a,点B表示的数为b,且A、B两点的距离是8.
(1)点A与点B之间(包括A、B两点)的整数有__________个;
(2)当a=-3时,b=_______;
(3)当![]() =5时,a=__________;
=5时,a=__________;
(4)当a取何值时, ![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(5)若![]() ,求a的范围.
,求a的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com