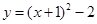练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    函数的最小值是（   ）
    A．1　 　B．－1　C．2　D．－2
    D

    试题分析：此函数的最小值，在x=-1时，y=-2，此时取最小值
    故选D
    点评：二次函数的解析式有三种形式：（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；（2）顶点式：y=a（x-h）2+k；（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，抛物线与x轴交A，B两点（A点在B点左侧），直线与抛物线交于A，C两点，其中C点的横坐标为2．

    （1）求A，B两点的坐标及直线AC的函数表达式；
    （2）P是线段AC上的一个动点，过P点作轴的平行线交抛物线于E点，求线段PE长度的最大值；
    （3）点G抛物线上的动点，在x轴上是否存在点F，使A，C，F，G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    若二次函数y=ax2+2x+a2-1(a≠0)的图象如图所示，则a的值是      

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知抛物线．
    （1）用配方法将化成的形式；
    （2）将此抛物线向右平移1个单位，再向上平移2个单位，求平移后所得抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

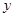    如图，点A的坐标为（－2，0），点B的坐标为（8，0），以AB为直径作⊙O′，交轴的负半轴于点C，则点C的坐标为       ，若二次函数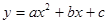的图像经过点A，C，B．已知点P是该抛物线上的动点，当∠APB是锐角时，点P的横坐标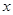的取值范围是           ．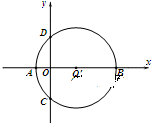

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

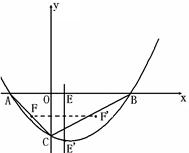
    如图1，二次函数的图象为抛物线，交x轴于A、B两点，交y轴于C点．其中AC=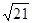，BC=，．
    （1）求二次函数的解析式；
    （2）若P点为抛物线上一动点且在x轴下方运动，当以P为圆心，1为半径的⊙P与直线BC相切时，求出符合条件的P点横坐标；
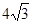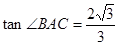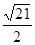    （3）如图2，若点E从点A出发，以每秒3个单位的速度沿着AB向点B匀速运动，点F从点A出发，以每秒个单位的速度沿着AC向点C匀速运动．两点同时出发，当其中一点到达终点时，另一点也随之停止运动．过点E作AB的垂线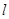交抛物线于点E′，作点F关于直线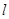的对称点F′．设点E的运动时间为t（s），点F′ 能恰好在抛物线吗？若能，请直接写出t的值；若不能，请说明理由．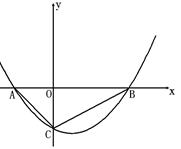
        
    图1                       图2                     

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    经营一批进价为2元一件的小商品，在市场营销中发现此商品的日销售单价（元）与日销售量y（件）之间关系为y=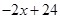，而日销售利润P（元）与日销售单价（元） 之间的关系为P=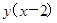．当日销售单价为多少时，每日获得利润48元，且保证日销售量不低于10件？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知二次函数的对称轴为，则        ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知，二次函数f(x)=ax2+bx+c的部分对应值如下表，则f(-3)=    。
    x
    		－2
    		－1
    		0
    		1
    		2
    		3
    		4
    		5
    y
    		5
    		0
    		－3
    		－4
    		－3
    		0
    		5
    		12

    查看答案和解析>>

    同步练习册答案