
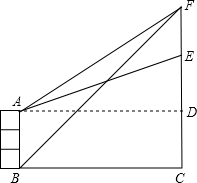
 如图所示,楼房AB的对面有一个建筑物EC.建筑物上方有一个信号发射塔EF.为测量EF的高度,某数学活动小组在B处测得塔尖F仰角为45°.在A处测得塔尖F仰角为α、测得点E仰角为β.已知AB高为10米,求EF的高度.(参考数据:tanα=$\frac{3}{4}$,tanβ=$\frac{9}{25}$)
如图所示,楼房AB的对面有一个建筑物EC.建筑物上方有一个信号发射塔EF.为测量EF的高度,某数学活动小组在B处测得塔尖F仰角为45°.在A处测得塔尖F仰角为α、测得点E仰角为β.已知AB高为10米,求EF的高度.(参考数据:tanα=$\frac{3}{4}$,tanβ=$\frac{9}{25}$) 分析 通过解等腰直角△BFC得到BC=FC,结合矩形的性质推知AD=BC;然后通过解直角△AFD与直角△EAD分别求得AD的长度;最后利用AD的长度不变列出方程求得FD、ED的长度,则EF=FD-ED.
解答  解:依题意得,AD=BC.
解:依题意得,AD=BC.
∵在直角△BFC中,∠FBC=45°,则BC=FC.
∴AD=FC=10+FD.
∵在直角△AFD中,∠FAD=α,tanα=$\frac{3}{4}$,
∴$\frac{FD}{AD}$=$\frac{3}{4}$,则AD=$\frac{4}{3}$FD.
∴10+FD=$\frac{4}{3}$FD.
解得FD=30.
∴AD=40米
∵在直角△EAD中,∠EAD=β,tanβ=$\frac{9}{25}$,
∴$\frac{ED}{AD}$=$\frac{9}{25}$,即$\frac{ED}{40}$=$\frac{9}{25}$,
∴ED=$\frac{72}{5}$(米),
∴EF=FD-ED=30-$\frac{72}{5}$=$\frac{78}{5}$(米).
答:EF的长度是$\frac{78}{5}$米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
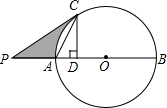 如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,
如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:填空题
菱形的对角线长分别为6和8,则此菱形的周长为__,面积为__.
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:填空题
一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com