
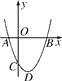
【题目】如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
【答案】③④
【解析】试题分析:先根据图象与x轴的交点A,B的横坐标分别为﹣1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,∴AB=4,∴对称轴x=﹣![]() =1,即2a+b=0.故①错误;②根据图示知,当x=1时,y<0,即a+b+c<0.故②错误;③∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,即c=﹣3a.故③正确;④∵△ADB为等腰直角三角形.所以AD=BD=
=1,即2a+b=0.故①错误;②根据图示知,当x=1时,y<0,即a+b+c<0.故②错误;③∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,即c=﹣3a.故③正确;④∵△ADB为等腰直角三角形.所以AD=BD=![]() AB,设D(1,a+b+c),又b=﹣2a,c=﹣3a,故D(1,﹣4a);列方程求解得a=1/2或a=﹣1/2(舍去),∴只有a=1/2时三角形ABD为等腰直角三角形,故④正确;⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣
AB,设D(1,a+b+c),又b=﹣2a,c=﹣3a,故D(1,﹣4a);列方程求解得a=1/2或a=﹣1/2(舍去),∴只有a=1/2时三角形ABD为等腰直角三角形,故④正确;⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣![]() ,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=
,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣
;同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣![]() 与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;同理当AC=BC时在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.经解方程组可知只有两个a值满足条件.故⑤错误.综上所述,正确的结论是③④.故答案是:③④.
;同理当AC=BC时在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.经解方程组可知只有两个a值满足条件.故⑤错误.综上所述,正确的结论是③④.故答案是:③④.


科目:初中数学 来源: 题型:
【题目】双 11 来了,剁手的脚步近了,去年“双 11”期间,自 11 日到 16 日累计进出港快递量达到 16089000 件,同比增长 69.36%,数据 16089000 用科学记数法表示为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A. 平均数B. 方差C. 中位数D. 极差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解题过程,回答问题. 如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,
所以∠BOC=∠MOD,
所以∠AOD=180°﹣∠BOC=180°﹣30°=150°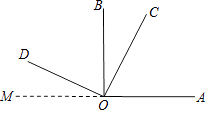
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接G20峰会,某校开展了“手绘G20作品”美术比赛,且作品的评分只有60分,70分,80分,90分,100分这五种结果.现随机抽取其中部分作品,对其份数及成绩进行整理统计,制作如下两幅不完整的统计图.
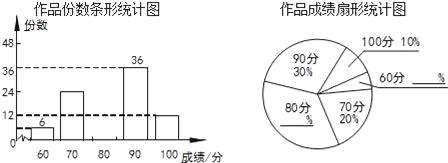
(1)本次共抽取了 份作品;
(2)其中得分为80分的作品所占的比例为 ,得分为70分的作品有 份;
(3)已知该校收到参赛的作品为1500份,估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x+3与直线y=-2x-1.
(1)若两直线与y轴分别交于点A,B,求点A,B的坐标;
(2)求两直线的交点C的坐标;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com